Matemàtiques (nivell ESO)/Àrees

L'àrea és una quantitat que expressa l'extensió d'una superfície o forma de dues dimensions al pla. L'àrea es pot entendre com la quantitat de material que seria necessària per crear un model de la forma, o la quantitat de pintura necessària per cobrir la superfície amb una sola capa. És l'analogia en dues dimensions de la longitud d'una corba (concepte unidimensional) i del volum d'un sòlid (concepte tridimensional).[1]
L'àrea d'una figura pot ser mesurada comparant la forma amb quadrats d'una mida fixa. En el Sistema Internacional d'Unitats (SI), la unitat estàndardd d'àrea és el metre quadrat (m2), que és l'àrea d'un quadrat els costats del qual mesuren un metre de llargada.[2] Una forma amb una àrea de tres metres quadrats tindria la mateixa àrea que tres d'aquests quadrats. En matemàtiques, el quadrat unitari es defineix com el que té una àrea igual a u. Pel que fa a la notació, si l'àrea correspon a una superfície plana se sol denotar com A, i si correspon a una superfície tridimensional se sol denominar S.[3]
Unitats de superfície
[modifica]
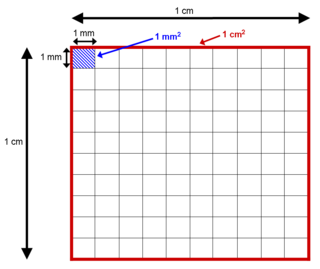
La unitat de mesura del Sistema Internacional per a mesurar l'àrea és el metre quadrat,[4] una unitat derivada definida a partir del metre.
Cada unitat de longitud té la seva corresponent unitat derivada de superfície; per als principals prefixos del Sistema Internacional s'obtenen les següents unitats.
- quilòmetre quadrat (km2) = 1.000.000 m2
- decímetre quadrat (dm2) = 0,01 m2
- centímetre quadrat (cm2) = 0,0001 m2
- mil·límetre quadrat (mm2) = 0,000001 m2
Una altra unitat no reconeguda pel Sistema Internacional però molt utilitzada és l'hectàrea, que és equivalent a un hectòmetre quadrat (1 hm2 = 10.000 m2) i a 100 àrees (1 àrea = 100 m2).
Hi ha altres unitats no oficials que s'usen en certs àmbits com el barn, d'ordre molt petit i que s'usa en l'àmbit nuclear. En el món agrari s'havien utilitzat moltes unitats, sovint pròpies d'un indret determinat, com per exemple la fanecada, la tafulla o la vessana]. En el Sistema Imperial d'Unitats (el sistema anglosaxó), la unitat base és la iarda quadrada, que equival a 0,83612736 m2; se'n deriven la polzada quadrada, el peu quadrat i l'acre, entre altres.
Fórmules
[modifica]Hi ha moltes fórmules conegudes per determinar les àrees de formes simples com triangles, rectangles i cercles. Fent ús d'aquestes fórmules es pot determinar l'àrea de qualsevol polígon dividint el polígon en triangles.[5]
Per a formes amb costats corbats se sol necessitar el càlcul per trobar l'àrea; de fet, el problema de determinar l'àrea de figures planes fou una gran motivació pel desenvolupament històric del càlcul.[6]
Per a una forma sòlida com una esfera, un con o un cilindre, l'àrea de la seva superfície externa s'anomena àrea superficial. Les fórmules per les àrees superficials foren trobades ja pels grecs antics, però esbrinar l'àrea de sòlids més complicats sol necessitar l'ús del càlcul amb múltiples variables.
Referències
[modifica]- ↑ Viquipèdia. Àrea
- ↑ Bureau International des Poids et Mesures. Resolution 12 of the 11th meeting of the CGPM (1960)
- ↑ Weisstein, Eric W. Chapman&Hall. CRC Concise Encyclopedia of Mathematics (en anglès), 1999. ISBN 0-8493-9640-9: p. 1763
- ↑ «Derived units expressed in terms of base units» (en anglès). BIPM. [Consulta: 4 de juny del 2011].
- ↑ Mark de Berg, Marc van Kreveld, Mark Overmars i Otfried Schwarzkopf (2000). Computational Geometry. Springer-Verlag, 2a revisada. ISBN: 3-540-65620-0 Capítol 3, Polygon Triangulation: pàg. 45–61.
- ↑ Carl B. (1959). A History of the Calculus and Its Conceptual Development. ISBN: 486606094
