Matemàtiques (Prova d'accés a cicles formatius de grau superior)/Els conjunts numèrics
Un nombre és el concepte que sorgeix del resultat de comptar les coses que formen un agregat, o una generalització d'aquest concepte.
Revisió dels nombres naturals, enters i racionals
[modifica]Els nombres naturals són els que es poden fer servir per a comptar els elements d'un conjunt. Per exemple: 24 pomes, 2 camions o 1123 peixos. Els altres tipus de nombres sorgeixen de successives generalitzacions d'aquest concepte.
Nombres naturals
[modifica]
Es fa servir el símbol (una N en doble ratlla) per a referir-se al conjunt de tots els nombres naturals. Alguns autors no consideren el zero (el nombre d'elements d'un conjunt que no en té cap) com un nombre natural. Per evitar ambigüitats sobre si s'inclou o no el zero, de vegades s'afegeix el subíndex "0" en el primer cas, i un superíndex "*" en l'últim:
- = { 0, 1, 2, ... } ; = { 1, 2, ... }.
Si no es posa cap subíndex s'ha d'entendre que es tracta del conjunt amb el zero inclòs.
Els nombres naturals es poden representar amb diferents tipus de notació, per exemple amb numeració romana, numeració en base 10 o numeració en base 2.
En el conjunt dels nombres naturals es defineixen les operacions de sumar, restar, multiplicar, dividir i elevar a una potència. Però el conjunt només és tancat respecte de les operacions de sumar, multiplicar i elevar a una potència. Això vol dir que el resultat de sumar, multiplicar o elevar a una potència dos nombres naturals és sempre un altre nombre natural. En canvi les operacions de restar i de dividir no sempre es poden fer, perquè no sembre existeix un nombre natural que doni el resultat de la operació.
Aquestes operacions dins del conjunt dels nombres naturals tenen les següents propietats:
| suma | multiplicació | |
| Propietat associativa: | a + (b + c) = (a + b) + c |
a × (b × c) = (a × b) × c |
| Propietat commutativa: | a + b = b + a | a × b = b × a |
| Existència de l'element neutre: | a + 0 = a | a × 1 = a |
| Propietat distributiva: | a × (b + c) = (a × b) + (a × c) | |
| No hi ha divisors de zero: | si ab = 0, llavors o bé a = 0 o bé b = 0 (o tots dos) | |
Els nombres naturals que no es poden dividir entre cap altre (tret de l'1) es diuen nombres primers.
Hi ha infinits nombres primers. Fixeu-vos que si ni hagués un nombre finit, els podríem multiplicar tots i al resultat sumar-li 1, però llavors obtindríem un nombre que no seria divisible entre cap nombre primer, per tant hauria d'haver un nombre primer diferent de tots que el dividís, altrament ell mateix seria primer.
Tots els nombres naturals diferents de zero que no son nombres primers es poden expressar com a producte de nombres primers. Això es diu descomposició en factors primers.
Teorema fonamental de l'aritmètica
[modifica]El teorema fonamental de l'aritmètica diu que aquesta descomposició existeix i és única.
La demostració té dues parts. Primer es demostra que tot nombre més gran que zero es pot escriure com a producte de factors primers i desprès que aquesta descomposició és única.
Existència.
Si existissin nombres que no es poguessin escriure com a producte de factors primers, llavors n'hi hauria un que seria el més petits de tots. Anomenem s aquest nombre. s no pot ser un nombre primer perquè si ho fos ell mateix seria la seva pròpia descomposició en factors primers, per tant s ha de ser un nombre compost. És a dir es pot escriure s=a•b per alguns nombres a i b més petits que s (això només és veritat si s és més gran que zero ja que zero es pot escriure com a producte de nombres iguals o més grans que zero per exemple 0=0·3). Però com que hem quedat que s és el més petit dels que no es poden descompondre en factors primers a i b sí que es poden descompondre, descomponent-los i substituint la seva descomposició a l'expressió s=a•b resulta que es pot trobar una descomposició en factors primers per a s. La única conclusió possible és que no hi ha cap nombre que no es pugui descompondre, és a dir tots es poden descompondre.
Unicitat.
El fet que la descomposició sigui única és una afirmació fàcil d'acceptar i des de l'antiguitat els matemàtics l'han donat per certa. Euclides pràcticament la va demostrar, però la primera demostració complerta no es troba fins a la publicació dels treballs de Gauss el 1801.
La dificultat de la demostració radica en que demostrar que la descomposició és única vol dir demostrar que per a cap nombre no n'hi pot haver dues de diferents. Per demostrar que una cosa existeix n'hi ha prou amb presentar un exemple però demostrar que quelcom no existeix és més difícil.
En els nombres naturals hi ha una estratègia per a demostrar que una cosa no existeix que es diu descens infinit. Es tracta d'aprofitar el fet que hi ha un nombre natural que és més petit que tots. És impossible que cap nombre natural tingui una determinada propietat si el fet que un la tingui obliga que un altre nombre natural estrictament més petit també la tingui. Perquè això permetria anar trobant nombres naturals cada cop més petits fins a trobar-ne de més petits que zero que no existeixen.
Si un nombre tingués dues descomposicions diferents, primer dividiríem el nombre i les dues descomposicions pels factors comuns i trobaríem un nombre amb dues descomposicions diferents sense cap factor comú entre elles. Sigui s aquest nombre ho ordenem de manera que escrivim els factors de petit a gran i el primer factor de la primera descomposició més petit que el primer de la segona llavors:
Dividint q1 entre p1 (ha de donar un residu diferent de zero perquè tots dos són nombres primers) es té q1=(d·p1 +r) i substituint:
Aplicant la propietat distributiva s'obté:
Restant a cada terme la quantitat dóna:
Tragent factor comú al segon terme:
Fixeu-vos que s'ha trobat un altre nombre que és estrictament més petit que s aquest nombre es pot expressar al mateix temps com el producte de p1 per i també com el producte dels factors a questes dues expressions pot ser que tinguin alguns factors comuns i es puguin divdir totes dues entre els factors comuns i també el nombre k però no tots els factors poden ser comuns perquè p1 no és a cap ki i és més gran que r. Per tant després d'haver dividit k i les dues descomposicions pels factors comuns s'haurà trobat un nombre k' més petit que s que també admet dues descomposicions ens factors primers. Tal com s'ha explicat abans això és impossible i per tant no existeix cap nombre s que admeti dues descomposicions diferents i per tant la descomposició que admeten tots els nombres més grans que zero és única.
Fixeu-vos que aquesta demostració no funcionaria si p1 fos zero, perquè no es pot dividir entre zero. Per això al teorema es diu que els nombres han de ser més grans que zero. De fet el zero admet infinites descomposicions diferents en producte de nombres naturals, per exemple:
Però no admet cap descomposició en producte de factors primers perquè a totes les descomposicions hi surt el zero que no és primer ja que és múltiple de tots els nombres (tots els nombres multiplicats per zero donen zero).
Màxim comú divisor i mínim comú múltiple
[modifica]El màxim comú divisor (mcd) de dos o més nombres naturals és, el major divisor possible de tots ells. Si el màxim comú divisor de dos nombres és 1, aleshores aquests nombres es diuen coprimers o primers entre ells.
Tot i que es pot anar provant nombres naturals un per un fins trobar el m.c.d., existeixen mètodes generals per trobar-lo.
- Descomponent tots els nombres en factors primers es prenen els factors comuns amb el seu menor exponent. Multiplicant aquests factors comuns es troba el màxim comú divisor.
Per exemple, de les factoritzacions de 6936 i 1200,
6.936 = 23 · 3 · 172 1.200 = 24 · 3 · 52
es pot inferir que el seu m.c.d. és 23 · 3 = 24
- Si algun dels nombres és molt gran, aquest mètode no és operatiu perquè pot ser difícil conèixer-ne els possibles factors. En eixe cas es pot fer servir l'algorisme d'Euclides.
L'algorisme d'Euclides es basa en la observació de que si un nombre a és divisor comú de altres dos b i c també és divisor comú del més petit dels dos i del residu de dividir el més gran entre el més petit. Fixeu-vos que si a és divisor comú de b i de c vol dir que existeixen dos nombres naturals b' i c' tals que b=b' ·a i c=c' ·c. expressant que:
on q és el quocient de dividir b entre c i r és el residu. D'aquí se'n dedueix que:
dividint els dos cantons entre a:
i restant als dos cantons c' ·q queda:
per tant a també és divisor de r (el resultat de dividir r entre a és un nombre natural). això permet transformar el problema de trobar el màxim comú divisor de b i c en el problema de trobar el màxim comú divisor de c i r ara es pot dividir c entre r si el residu és 0 el màxim comú divisor és r si el residu no és zero es pot tornar a repetir el mateix emrant c en comptes de b i r en comtes de c i així successivament.
Per exemple, per trobar el màxim comú divisor de b = 945 i c = 651:
945 = 1×651 + 294
651 = 2×294 + 63
294 = 4×63 + 42
63 = 1×42 + 21
42 = 2×21 + 0 llavors mcd(945; 651) = 21 (l'últim residu no nul).
- Geomètricament, el màxim comú divisor de a i b és el nombre de punts de coordenades enteres que hi ha en el segment que unix els punts (0, 0) i (a, b), excloent el (0, 0). Vegeu figura de la dreta.
Mínim comú múltiple El mínim comú múltiple (m.c.m.) de dos o més nombres naturals és, el menor nombre enter que és múltiple de tots ells.
- Un mètode general per calcular el mínim comú múltiple de dos o més nombres consisteix en descompondre els nombres en factors primers i després prendre els factors comuns amb el major exponent amb què apareguin i els factors no comuns també amb el seu major exponent. Multiplicant tots aquest factors es troba el m.c.m.
Per exemple, de les factoritzacions de 6.936 i 1.200,
6.936 = 23 · 3 · 172 1.200 = 24 · 3 · 52
se'n pot inferir que el seu m.c.m. és 24 · 3 · 52 · 172 = 346.800.
El mínim comú múltiple de dos nombres i el màxim comú divisor estan lligats per la relació: m.c.d.(a, b)·mcm(a, b) = ab. Fixeu-vos que si s'agafen tots els factors al màxim exponent (mcm) i els factors comuns al mínim exponent (mcd) és igual a agafar tots els factors al màxim exponent i al mínim és a dir tots els factors del primer número i tots els del segon per tant és el mateix que multiplicar-los. Això permet trobar el mínim comú múltiple a partir del màxim comú divisor:
Per tant es pot trobar primer el màxim comú divisor emprant l'algorisme d'Euclides i llavors trobar el mínim comú divisor dividint el producte dels dos nombres entre el màxim comú divisor.
Per exemple en el cas de 6.936 i 1.200 es té:
Nombres enters
[modifica]A partir dels nombres naturals es construeixen els nombres enters estenent-los, és a dir afegint-los-hi uns nous elements que cal inventar-los per tal que la resta sempre tingui un resultat.
La resta es defineix com la operació inversa de la suma, així si llavors i .
El conjunt dels nombres naturals es diu que és tancat respecte de la suma perquè per a qualsevol parella de nombres naturals, el resultat de la seva suma és també un nombre natural.
Ara bé, resulta que el conjunt de nombres naturals no és tancat respecte de la resta perquè, per exemple, no existeix cap nombre natural que sumat a 1 doni zero, per tant 0-1 no té cap resultat dins del conjunt dels nombres naturals.
El nombre negatiu -n ( oposat de n) es defineix com el nombre que sumat a n dóna zero.
Els nombres negatius es poden interpretar com la quantitat d'elements, de conjunts amb elements especials, que en unir-se amb els conjunts que tenen elements normals es neutralitzen o cancel·len o anul·len. Per exemple una quantitat negativa de diners es pot emprar per a representar un deute de tal manera que en unir-se amb la mateixa quantitat però positiva es cancel·la el deute. La càrrega elèctrica d'un determinat nombre de partícules es pot representar amb un nombre negatiu de tal manera que en reunir-se amb un nombre igual de partícules que tenen la mateixa quantitat de càrrega però oposada es cancel·len mútuament i en resulta una matèria elèctricament neutra.
Els nombres negatius s'escriuen afegint un signe menys davant del nombre del qual en són oposats. Així l'oposat del 7 s'escriu −7. Quant el conjunt de nombres negatius s'uneix amb el conjunt dels nombres naturals (inclòs el zero), s'obté el conjunt dels nombres enters Z (Del alemany Zahl, plural Zahlen, que vol dir nombre), també s'escriu com a .
Es defineix el valor absolut d'un nombre enter n de la següent manera: Si el nombre n és positiu el seu valor absolut és el mateix nombre, si és negatiu el seu valor absolut és el seu oposat (és a dir el nombre positiu que cal sumar-li perquè el resultat sigui zero).
Operacions amb nombres enters.
Cal definir que vol dir sumar, restar, multiplicar i dividir dos nombres negatius o un nombre negatiu amb un nombre positiu (operar dos nombres positius ha de ser el mateix que fer-ho amb dos nombres naturals).
Extensió de la suma.
En sumar dos nombres negatius si es vol que es conservin les propietats commutativa i associativa ha de ser:
Per tant cal definir la suma com:
O dit en paraules, per sumar dos nombres negatius, se sumen els mòduls i al resultat se li posa signe negatiu.
Llavors es pot veure que sumar un nombre negatiu i restar han de ser el mateix. Com que en sumar i restar el mateix nombre a una quantitat ha de quedar la mateixa quantitat, si s’ha de seguir complint la propietat associativa ha de ser:
Aquesta propietat permet definir la suma de dos nombres de diferent signe. Si el que té el mòdul més gran és el positiu i el que té el mòdul més petit és negatiu simplement es resta del de mòdul més gran el més petit. Si el que té el mòdul més gran és el negatiu llavors no es pot restar però es pot aplicar el següent:
Per tant el que es fa és restar del que té el mòdul més gran el que el té més petit i al resultat se li assigna signe negatiu.
Extensió de la resta.
Com que sumar un nombre negatiu i restar ha de ser el mateix, per estendre la resta n’hi ha prou amb definir-la com la suma de l’element oposat. Llavors s’apliquen les regles de la suma.
Extensió de la multiplicació.
Per estendre la multiplicació al cas de dos nombres de diferent signe es pot forçar que es compleixi la propietat commutativa per poder multiplicar sempre el positiu pel negatiu i definir-la com el resultat de sumar el negatiu amb si mateix una quantitat de vegades igual al nombre positiu. Això és el mateix que sumar el positiu amb si mateix una quantitat de vegades igual al mòdul del nombre negatiu i al resultat canviar-li el signe. O el que és el mateix multiplicar els mòduls i al resultat assignar-li el signe negatiu.
L'observació anterior dóna el criteri per estendre la multiplicació de dos nombres negatius es multiplica un pel mòdul de l’altre (que com que el primer és negatiu dóna un resultat negatiu) i al resultat se li canvia el signe (que dóna un resultat positiu).
Extensió de la divisió.
Si es vol que en tornar a multiplicar el resultat d'una divisió pel divisor doni altre cop el dividend no hi ha més remei que definir-la com el resultat de la divisió dels mòduls i llavors aplicar el mateix criteri de signes que amb la multiplicació. Cal fixar-se que igual com passa amb els nombres naturals, no sempre es pot trobar el resultat d’una divisió, és el cas en què no es pot trobar el resultat de la divisió dels mòduls en el conjunt dels nombres naturals.
Resum
Tot això es pot resumir en la següent taula on a i b són nombres naturals:
| Sumar | Restar | Multiplicar | Dividir | |
|---|---|---|---|---|
| a, b | a+b | a-b=a-b si a>b
a-b=-(b-a) si b>a |
a·b | a/b |
| a, -b | a+(-b)=a-b si a>b
a+(-b)=-(b-a) si b>a |
a-(-b)=a+b | a·(-b)=-(a·b) | a/(-b)=-(a/b) |
| -a, b | (-a)+b=b-a si b>a
(-a)+b=-(b-a) si a>b |
(-a)-b=-(a+b) | (-a)·b=-(a·b) | (-a)/b=-(a/b) |
| -a, -b | (-a)+(-b)=-(a+b) | (-a)-(-b)=b-a si b>a
(-a)-(-b)=-(a-b) si a>b |
(-a)·(-b)=a·b | (-a)/(-b)=a/b |
O els que és el mateix amb les següents regles:
- Per sumar dos nombres enters
- del mateix signe: Se sumen els valors absoluts dels sumands, es posa el mateix signe dels sumands.
- de diferent signe: Es resten els valors absoluts dels sumands, es posa el signe del sumand que té el major valor absolut.
- Per restar dos nombres enters se suma el primer a l'oposat del segon.
- Per multiplicar dos nombres enters: Es multipliquen els valors absoluts dels factors, Si són del mateix signe es posa signe positiu si són de diferent signe es posa signe negatiu.
- Per dividir dos nombres enters: Es divideixen els seus valors absoluts, Si són del mateix signe es posa signe positiu si són de diferent signe es posa signe negatiu.
Relació d'ordre Un cop definida la resta es pot definir una relació d'ordre en eo conjunt dels nombres entres. Un nombre a és més gran o igual que un nombre b si a-b és un nombre natural (un enter no negatiu).
Per exemple (-3) és més gran o igual que (-7 ) perquè (-3)-(-7) = 4 que és un nombre natural. En canvi (-7) no és més gran que 6 perquè (-7)-6 = -13 que no és un nombre natural.
Extensió de la potenciació.
Estendre la operació de elevar un nombre negatiu a un exponent positiu no té cap problema un cop s’ha estès la multiplicació de nombres negatius. Només fixeu-vos que com que cada cop que el nombre es multiplica per si mateix canvia el signe el resultat serà el mateix que elevar el mòdul del nombre però amb signe negatiu si l’exponent és senar i positiu si l’exponent és parell.
Cal resoldre el problema de donar un significat a la operació de elevar un nombre a un exponent negatiu. Elevar-lo a un exponent positiu volia dir multiplicar-lo per si mateix tantes vegades com indica l’exponent però què pot voler dir multiplicar-lo per si mateix un nombre negatiu de vegades?
La forma de resoldre-ho és observar la següent propietat de la potenciació en nombres naturals:
Si es vol que la mateixa propietat es conservi pel cas dels nombres enters s’ha de fer que:
Però fixeu-vos que
Per tant s'ha de definir la potència a un exponent negatiu com la divisió entre la potència al mateix exponent positiu:
Fixeu-vos que encara que el conjunt dels nombres naturals era tancat respecte de la potenciació, el conjunt dels nombres enters no ho és perquè hi ha potències que no tenen solució al conjunt dels nombres enters per exemple:
Que no és un nombre enter. Això permet també donar sentit a l'operació de elevar a la potència zero de la següent manera:
D'aquesta manera convé assignar el valor 1 a qualsevol nombre elevat a zero.
Nombres racionals
[modifica]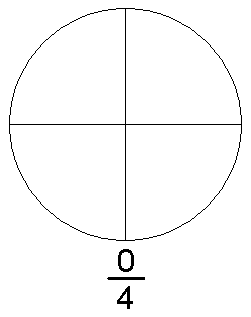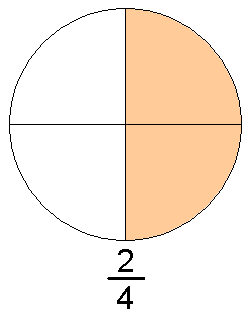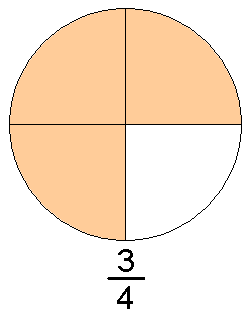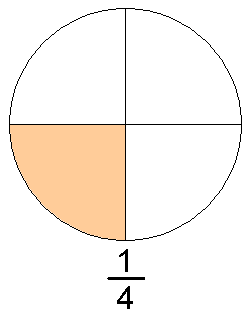
Igual com s'estén el conjunt dels nombres naturals per tal de que la operació de restar tingui sempre un resultat, en estendre el conjunt dels nombres enters per tal que la operació de dividir tingui sempre un resultat s'obté el conjunt dels nombres racionals.
Un nombre racional és el que es pot expressar com a una raó entre dos nombres enters. És a dir el quocient d'una quantitat (dita antecedent) dividida per una altra quantitat (dita conseqüent) que no pot ser zero.
Una raó es pot escriure com una fracció amb un numerador enter i un denominador natural diferent de zero.
La fracció m/n o
Representa la mida de reunir m parts iguals tals que cada una d'aquestes parts té una grandària tal que n parts juntes tenen la mateixa mida que la unitat. Dues fraccions diferents poden correspondre al mateix nombre racional; per exemple 1/2 i 2/4 són iguals, és a dir:
- .
Si el valor absolut de m és més gran que n, llavors el valor absolut de la fracció és més gran que 1. Les fraccions poden ser més grans que, més petites que, o iguals a 1 i també poden ser positives, negatives o zero. El conjunt de totes les fraccions inclou els enters donat que tot enter pot ser escrit com una fracció amb denominador 1. Per exemple −7 es pot escriure −7/1.
El símbol per a representar el conjunt dels nombres racionals és Q (de quocient), també s'escriu .
Fraccions equivalents Si a partir d'una fracció a/b s'obté un altre fracció multiplicant el numerador i el denominador per mateix nombre c s'obté una nova fracció que es pot entendre com el resultat de dividir una unitat en un nombre c·b de bocins iguals i agafar-ne c·a d'aquests bocins però cada c bocins tenen la mateixa quantitat que in dels bocins d'abans per tant al final s'ha agafat el mateix. Aquestes dues fraccions es diuen fraccions equivalents, i les dues representen el mateix nombre racional.
Pel mateix motiu si es divideix numerador i denominador entre el mateix nombre s'obté un altre fracció equivalent. Si es divideixen tots dos pel màxim comú denominador, s'obté la fracció equivalent que té el nombre més petits possibles. Aquesta fracció es diu fracció irreductible
Representació decimal dels nombres racionals
El sistema de numeració decimal s'estén per a representar els nombres racionals a base d'afegir una coma (als Estats Units i al Regne Unit en comptes d'una coma s'empra un punt) que separa la part entera de la part decimal del nombre. Els dígits de la dreta de la coma representen la quantitat de dècimes, centèsimes, mil·lèsimes etc.
Tot nombre racional té una representació decimal que o bé s'acaba o bé arriba un punt on una seqüència de xifres, anomenada període, es repeteix infinitament. Per exemple 1/2=0.5 o 1/3 = 0,3333.... o 157/13=12,076923 076923 076923... 076923...
Això és fàcil de veure amb l'algorisme de la divisió, el residu de dividir el nombre ha de ser necessàriament més petit que el quocient, per a calcular la primera xifra decimal es multiplica per deu el residu i es divideix pel quocient si el nou residu és zero ja s'ha acabat, si és igual que l'anterior residu la xifra decimal es repeteix infinitament. Si és diferent de l'anterior residu es continua l'algoritme, però la quantitat de nombres diferents més petits que el quocient és finita per tant tard o d'hora es repetirà un residu i a partir d'aquí la successió de xifres decimals es repetirà infinits cops.
Pas de la representació decimal d'un nombre racional a la representació amb fraccions
La millor manera d'explicar-ho és amb un exemple:
Sigui a = 12,345 67 67 67 67 67 ...
Es repeteixen dues xifres; multipliquem a per 102 = 100.
100a = 1234, 567 67 67 67 67 ... a = 12, 345 67 67 67 67 ...
En sostreure, se'n va tota la part periòdica:
100a - a = 1222,22 llavors
(100-1)a = 1222,22
99a = 1222,22
Com que hi ha dos decimals es multiplica per cent als dos costats i queda:
100·99a = 100·1222,22 9900a = 122222
I dividint entre 9900 els dos cantons
a = 122222/9900
Operacions aritmètiques amb nombres racionals
Suma si dues fraccions tenen el mateix denominador (la unitat s'ha partit en el mateix nombre de parts iguals) la forma natural de sumar-les (de trobar una fracció que representi una quantitat equivalent a la unió de les quantitats que representaven cada una de les fraccions que es vol sumar) és sumant els numeradors i mantenint el mateix denominador.
En cas de fraccions amb diferent denominador, qualsevol mètode que permeti trobar fraccions equivalents a les originals però que tinguin el mateix denominador permetrà aplicar el criteri que s'ha explicat abans per a fraccions amb el mateix denominador.
En multiplicar el numerador i el denominador d'una fracció per un mateix nombre n s'obté un altre fracció equivalent a la primera (que representa el mateix nombre racional). Això es pot veure acudint a la definició de fraccions o simplement de forma intuïtiva veient que si la unitat es parteix entre un nombre de parts que és el doble o el triple o n cops el denominador inicial però al mateix temps s'agafa el doble o el triple o n cops el numerador inicial, al final es té la mateixa quantitat.
Acudint a la definició de fraccions equivalents:
Això dóna diversos mètodes per obtenir faccions amb el mateix denominador però el més senzill d'explicar és multiplicar el numerador i el denominador de la primera fracció pel denominador de la segona i multiplicar el numerador i el denominador de la segona pel denominador de la primera:
Exemple:
Resta
Primer cal definir l'element oposat. Cal que la definició es faci de manera que la suma de qualsevol racional amb el seu oposat doni zero:
Llavors es defineix la resta com la suma amb l'element oposat:
Exemple:
Multiplicació primer fixeu-vos que si es tracta de multiplicar un nombre natural n per un nombre racional, intuïtivament, es tractaria sumar el nombre racional amb si mateix n cops, per tant hauria de ser:
El que no és tan immediat d'interpretar és al multiplicar-lo per un nombre fraccionari, per exemple 1/n. Quin sentit pot tenir sumar un nombre amb si mateix 1/n cops? La idea per donar sentit a aquest concepte consisteix en buscar la solució que permeti mantenir la propietat associativa, si es vol que:
S'ha de definir de forma que perquè per tant cal definir:
- . (perquè )
I per tant:
Per exemple:
Divisió
L'element invers es defineix com:
Com en el cas anterior la definició cal fer-la així perquè el producte s'un element pel seu invers doni 1:
S'ha de prohibir l'invers d'una fracció amb zero al numerador perquè al seguir la regla quedaria una fracció amb zero al denominador que al definir els nombres racionals es va haver de prohibir.
Llavors la divisió es defineix de forma habitual com el producte per l'element invers:
Exemple:
Potenciació
Per estendre la potenciació als nombres racionals cal definir el concepte de elevar a una potència fraccionària.
Fixeu-vos que:
Per tant:
Però
En general
Això que es cert pel cas que el numerador sigui múltiple del denominador es pot fer servir com a definició per donar sentit a la potència quant l’exponent és un nombre fraccionari de forma que:
Els nombres racionals no són tancats respecte de la potenciació, perquè hi ha potències que no es poden calcular, per exemple no existeix cap nombre racional a/b que sigui igual a 21/2
Si existís, per demostrar-ho n’hi hauria prou amb escriure la fracció, elevar-la al quadrat i veure que dóna 2. Per demostrar que no n’hi ha cap cal emprar alguna tècnica una mica més complicada, per exemple es pot demostrar per descens infinit però per veure una tècnica diferent ho farem per reducció al absurd. La tècnica de la reducció al absurd consisteix en suposar que una determinada propietat es compleix i a partir d’aquí arribar a una contradicció (que una cosa és veritat i mentida al mateix temps) com que això no pot ser, llavors la propietat no es pot complir.
Se suposa que existeix un nombre racional, la fracció irreductible del qual és a/b tal que el seu quadrat és 2. És a dir:
Però llavors multiplicant per b2 als dos cantons resulta que:
Per tant a2 és múltiple de 2 i en conseqüència a també, és a dir hi ha un nombre natural a' tal que a=2a' i a2=4a' 2 Subsituint a2 per aquest valor i dividint entre dos als dos cantons de la igualtat resulta:
Per tant b també ha de ser parell. Però això és una contradicció amb la hipòtesi de que a/b era una fracció irreductible. Per tant no pot haver-hi cap nombre racional tal que el seu quadrat sigui 2, o dit d’altra manera 21/2 no es pot calcular en el conjunt dels nombres racionals.
Relació d'ordre
Si a i b són dos nombres racionals es diu que a ≥ b (i es llegeix a és més gran o igual que b) si i només si a - b és no negatiu.
Exemple:
Es compleix que aquesta relació d'ordre és total perquè a - b = - (b - a) i també es compleix que si a ≥ b i b ≥ a ha de ser a = b perquè ha de ser a - b =0.
Propietat de densitat
Amb aquesta relació d'ordre es diu que el conjunt dels nombres racionals és dens. Això vol dir que per a qualsevol parella de nombres racionals existeix algun altre nombre racional situat entre els dos. Fixeu-vos que això no passa amb els conjunts dels nombres naturals i dels nombres enters.
Demostració
Donats dons nombres racionals qualsevol r1 i r2 es tracta de trobar un nombre racional que estigui entremig. Per tant per demostrar la propietat n'hi ha prou amb demostrar que (r1 + r2)/2 és racional i esta entremig dels dos.
- (r1 + r2)/2 és racional
Si
llavors
que és un nombre racional perquè tant el numerador com el denominador són nomres enters i el denominador és diferent de zero.
Ara, suposant que r1 ≤ r1, cal veure que aquest resultat és més gran o igual que r1 i més petit o igual que r2
Si r1 ≤ r2 vol dir que
Però
que és no negatiu, per tant r1 ≤ (r1 + r2)/2
Que és el mateix d'abans, per tant tampoc és negatiu i per tant queda demostrada la propietat.
Quants nombres racionals hi ha?

Per contestar aquesta pregunta cal posar-se d'acord amb què vol dir quantitat d'elements en el cas de conjunts que en tenen infinits. En el cas de conjunts finits per dir quants elements té el que es fa és contar-los. Per contar-los s'identifiquen un a un de forma que no es repeteixin i a cada un se li assigna un nombre natural per ordre creixent començant per l'1 . L'últim nombre assignat és el nombre d'elements del conjunt.
En el cas dels conjunts amb un nombre infinit d'elements també es pot plantejar la idea de assignar-li a cada un un nombre natural. Evidentment si la quantitat d'elements del conjunt no s'acaba mai no hi haurà un últim nombre assignat. Per tant lo únic que es pot pensar és que si aquesta assignació és factible llavors la quantitat de elements és tan infinita com la quantitat de nombres naturals, si no es pot fer, llavors es pot pensar si és un infinit més gran o més petit que l'infinit de la quantitat de nombres naturals.
En fer això apareixen resultats que poden semblar sorprenents. Per exemple el conjunt dels nombres parells a primer cop d'ull sembla que tingui una infinitat d'elements més petita que el conjunt de tots els nombres naturals. Però en mirar-ho amb més detall resulta que no. Fixeu-vos que a cada nombre parell se li pot assignar un nombre natural que és el resultat de dividir-lo per dos. Fent això a cada nombre parell li correspon un i només un nombre natural i a cada nombre natural li correspon un i només un nombre parell. Per tant no hi ha cap motiu per poder afirmar que cap dels dos conjunts tingui una infinitat d'elements més gran que l'altre.
Els conjunts que tenen una infinitat d'elements tan gran com la dels nombres naturals es diu que són conjunts numerables.
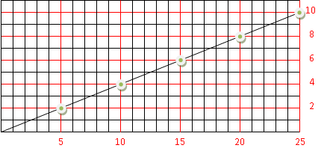
Dons bé, resulta que el conjunt dels nombres racionals és un conjunt numerable. Per veure-ho només cal que us fixeu amb el gràfic de la dreta. Si es van assignant els nombres naturals començant per l'1, després el 2 i així successivament als nombres de color negre seguint l'ordre de les fletxes, resulta que a cada nombre natural se li assigna un i només un nombre racional i a cada nombre racional se li assigna un i només un nombre natural.
Més endavant s'estudiaran conjunts infinits que no són numerables i que tenen una infinitat de elements més gran que la dels nombres naturals.
ES VERITAT!!!
Els nombres irracionals
[modifica]Suposeu que l'espai i el temps es poguessin dividir en bocins tan petits com es vulgues. Com que els nombres racionals també es poden fer tan petits com es vulgui, sembla que podrien ser una eina adequada per representar mesures d'aquestes magnituds. Però això no està del tot clar.
Si tan sols es tracta de dividir una longitud entre un nombre enter de bocins (tants com es vulgui) sí que ens han d'anar bé, però vegem que passa amb una versió una mica modificada de la famosa cursa entre Aquil·les i la tortuga.
Suposem que Aquiles li dóna un metre d'avantatge a la tortuga, que la tortuga va a una velocitat constant d'1 metre per hora, i posats a suposar, suposeu que Aquil·les per burlar-se'n de la pobre bèstia decideix fer un sorteig i tria un nombre al atzar entre l’1 i el 9, calcula el temps que la tortuga tardarà en recorre aquest nombre de decímetres i modera la seva velocitat per tal de recorre el primer metre de forma que quant Aquil·les l'hagi recorregut la tortuga hagi avançat exactament aquests decímetres. Per exemple si ha sortit 5 vol dir que la tortuga tardarà mitja hora en recórrer els 5 decímetres llavors Aquil·les corre a una velocitat de mig metre per hora (encara que s'hagi d'avorrir força). Un cop Aquil·les ha arribat al punt on estava la tortuga repeteix el procés però ara només li deixa avançar uns pocs centímetres (els que surtin d'un altre sorteig), després mil·límetres i així successivament. Fixeu-vos que suposant que Aquil·les no triga gens en fer els càlculs, prendre la decisió i canviar de velocitat:
- La velocitat màxima a que ha de córrer Aquil·les es perfectament factible, en el pitjor cas en què en una etapa hagi sortit 9 i en la següent surti 1, Aquil·les haurà de recorre 9 unitats d'espai en el temps que la tortuga corri 1 dècima part d'una d'aquestes unitats és a dir Aquil·les haurà d'anar 90 vegades més ràpid que la tortuga 1 metre per hora x 90 = 90 metres per hora. Fins i tot en aquest cas s'avorrirà força ell que pot anar a més de 36 km/h.
- Més aviat d'hora que no pas tard Aquil·les es menjarà una bona sopa de tortuga (fa 3500 anys les tortugues no estaven en perill d'extinció). Fixeu-vos que la tortuga com a màxim arribarà a recórrer 2 metres (al primer metre li afegim com a màxim 9 decímetres, després com a màxim 9 centímetres... ) i la velocitat mínima a que anirà Aquil·les es més gran que 1 metre per hora, (Aquil·les sempre va més despresa que la tortuga) per tant en menys de dues hores podrà començar a preparar la seva sopa de tortuga.
Dons bé resulta que la longitud recorreguda per la tortuga en el moment que Aquil·les la atrapa pot molt ben ser que no es pugui representar amb un nombre racional. Fixeu-vos que serà una longitud que s'apressarà amb un nombre decimal format per un 1 seguit d'una quantitat infinita de decimals que no tenen perquè repetir-se mai.
Però resulta que tots els nombres racionals tenen una representació decimal que a partir d'un noment donat les seves xifres es repeteixen (de vegades la xifra que es repeteix es el zero). Per tant resulta que aquesta distància no és sempre un nombre racional.
Si suposem que l'espai real es pot dividir fins a d'infinit llavors cal inventar un nou tipus de nombres per poder mesurar les longituds en aquest espai real. A aquests nombres s'anomenen nombres reals.
Els nombres reals que no són racionals s'anomenen nombres irracionals.
Fixeu-vos que amb l‘algorisme de calcular l'arrel quadrada es poden anar calculant més i més decimals de la arrel quadrada de 2. Per tant la arrel quadrada de dos és un d'aquests nombres reals que no és racional i per tant és irracional.
Hi ha molts més nombres irracionals que no pas nombres racionals.
Per poder explicar-ho primer cal veure que els nombres reals no es poden contar, quant hàgiu llegit la part dels nombres reals torneu a llegir el que segueix.
El nombre pi és un nombre irracional
El temari està ordenat tal com es descriu a la prova d'accés, però per poder explicar aquesta part primer cal que hageu llegit trigonometria i derivades desprès torneu a llegir el que segueix
El nombre e és un nombre irracional
El temari està ordenat tal com es descriu a la prova d'accés, però per poder explicar aquesta part primer cal que hageu llegit logaritmes, derivades i integrals (integrals no surt al programa però s'afegeix al llibre per poder explicar aquesta part i d'altres que sí que hi surten). Després torneu i llegiu el que segueix.
Conjunt de nombres reals
[modifica]Un camí per seguir ampliant els conjunts de nombres és fer que el conjunt sigui tancat respecte de la inversa de la potenciació. Aquest camí porta a resultats força interessants però no és el camí que porta als nombres que s'estudiaran aquí. Ja s'ha explicat per poder explicar els nombres irracionals que perquè els nombres puguin representar un hipotètic espai real infinitament divisible cal ampliar els nombres racionals.
Fixeu-vos que el que s'ha fet a la cursa d'Aquil·les i la tortuga ha estat crear una llista infinita de nombres racionals: primer 1, després 1,d on d és la xifra dels decímetres, després 1,dc on c és la xifra dels centímetres i així successivament. Aquesta llista es pot numerar amb els nombres naturals, es pot dir que el primer terme de la llista és 1, els segon és 1,d i així successivament. Una llista de nombres ordenada i numerada amb els nombres naturals es diu que és una successió cada nombre es diu que és un terme de la successió, el terme genèric corresponent a un nombre natural qualsevol n normalment es designa com an.
La successió que s'ha construït en el cas de la cursa es correspon amb un punt de l'espai: el punt on Aquil·les atrapa la tortuga. Però no totes les successions que es poden construir d'aquesta forma es corresponen amb punts de l'espai, per exemple si fos la tortuga qui perseguís a Aquil·les la distància entre ells es faria cada cop més gran i no s'arribarien a trobar mai.
Una propietat de la successió inicial és que els nombres estaven cada cop més a prop l'un de l'altre, mentre que a la segona successió (la que sortiria si fos la tortuga qui perseguís a Aquil·les) els nombres estarien cada cop més separats. Que els nombres estiguin cada cop més junts és necessària però no n'hi ha prou, fixeu-vos amb la següent successió:
Els seus termes estan cada cop més junts, de fet la distància entre un terme i el següent si es va prou lluny es fa tan petita com es vulgui:
Però aquesta successió no convergeix, si representés la distància recorreguda per dos objectes que es persegueixen no es trobarien mai.
Fixeu-vos que passa si per un determinat an amb n= 2 + 2m s'agrupen els termes de la següent manera:
Els dos sumands inicials donen 1,5 després cada conjunt de sumands entre parèntesis dóna un nombre més gran que 1/2. Fixeu-vos que el primer parèntesi té 2 dos sumands que són més grans o iguals que 1/4 per tant dóna més de 1/2, el segon parèntesi té 4 sumands i tots són més grans o iguals que 1/8 per tant dóna més de 1/2, i així successivament fins a l'enèsim parèntesi que té 2n-1 sumands i tots són més grans o iguals que 1/2n i per tant també és més gran que 1/2:
Queda clar que a base de triar un valor de n prou gran la successió creix tan com es vulgui.
Si una successió s'obté a base d'anar sumant quelcom al terme anterior es diu sèrie en aquest cas es tracta d'una sèrie molt coneguda que s'anomena sèrie harmònica.
S'ha vist que la condició de que els elements de la successió s'apropin no és suficient per poder assignar un punt de la recta a la successió, el problema ha sorgit pel fet que a base d'agafar-ne cada cop més acaben afegint una distància cada cop més gran. Per tant per garantir que es pot assignar un punt a la successió cal exigir que a partir d'un moment donat la distància entre qualsevol parella de punts (no només l'últim i l'anterior) es va fent cada cop més petita. Si una successió compleix aquesta condició es diu que és una successió de Cauchy Una forma d'enunciar això és tal com segueix:
Es diu que una successió és de Cauchy si i només si per tot èpsilon positiu (per petit que sigui) existeix un (encara que calgui triar-lo molt gran) tal que si i són més grans que aleshores es compleix que el valor absolut de (és a dir, el mòdul, si és positiu és el mateix valor i si és negatiu és el valor canviat de signe) és més petit que èpsilon. Escrit formalment es pot expressar de la manera següent: Sigui el conjunt de totes les successions de Cauchy, llavors:
I es llegeix així: Una successió Xn pertany al conjunt de les successions de Cauchy (Sc) si i només si per a tot ε més gran que 0 existeix un n0 pertanyent al conjunt dels nombres naturals tal que si n i m compleixen la condició de ser més grans o iguals que N 0 llavors el mòdul de Xm- Xn és més petit que ε.
Successions convergents
Es diu que una successió és convergent o també que té un límit finit l si existeix un nombre l tal que els termes de la successió s'apropen a l tant com es vulgui, és a dir que si es vol que s'apropin més que un nombre molt petit ε sempre es pot trobar un nombre prou gran N0 de forma que a partir de n>N0 tots els an estàn més a prop de l que una distància ε és a dir la distància entre an i l és més petita que ε (en els nombres racionals la distància es mesura restant-los i obtenint el mòdul, és a dir si el resultat de la resta té signe positiu deixant-lo i si té signe negatiu canviant-lo per positiu). Quant una successió an té límit l també es diu que el límit de an quan n tendeix a infinit és l i s'escriu:
Emprant aquesta notació i els símbols de lògica matemàtica la definició de límit d'una successió es pot escriure:
i es llegeix: el límit de la successió an quan n tendeix a infinit és igual a l si i només si per a tot ε més gran que zero existeix un N0 tal que per a tot n més gran que N0 el mòdul de la diferència entre l i an és més petit que ε.
Extensió dels nombres racionals per obtenir els nombres reals
Fixeu-vos que al conjunt dels nombres racionals no totes les successions de Cauchy tenen límit (cas de la cursa entre Aqui·les i la tortuga o de la successió d'anar trobant decimals de l'arrel quadrada de 2, en canvi en l'espai de la línia recta contínua sí que hi ha un punt que es pot assignar a cada successió de Cauchy.
Es tracta de fer quelcom semblant al que s'ha fet amb l'extensió dels nombres enters per obtenir els racionals. Recordeu que els enters no eren tancats respecte de trobar el quocient de dos nombres i s'estenen inventant les fraccions que són parelles de nombres dels quals es vol trobar el quocient. Però resultava que moltes parelles corresponien al mateix nombre (recordeu les fraccions equivalents) llavors es feia que els nombres racionals fossin el que tenen en comú totes les fraccions equivalents a una donada, per exemple la fracció irreductible.
Es tracta de estendre el conjunt dels nombres racionals de manera que s'obtingui un conjunt que sigui tancat respecte de l'operació de trobar el límit d'una successió de Cauchy. Es pot inventar un nou conjunt de nombres que estiguin representats precisament per les successions de Cauchy però resulta que (igual que passava amb les fraccions) hi ha moltes successions de Cauchy que tenen el mateix límit. Per això es diu que dues successions de Cauchy an i bn són equivalents (de forma anàloga a les fraccions equivalents en els nombres racionals) si la successió cn (que es construeix restant els temes dos, és a dir de forma que cn = an - bn per a tot n) tendeix cap a zero. Com que zero és un nombre racional no hi ha problema en verificar si la successió diferència de dues successions té aquest límit encara que cap de les dues tingui límit en els racionals.
A diferencia del cas de les fraccions on hi ha una fracció irreductible, en les successions no es pot trobar una successió irreductible tot i que si es treballa en base 10 n'hi ha una que sovint es fa servir per identificar el nombre:
on m és un nombre enter i di són xifres del 0 al 9 que es diuen els dígits de la representació decimal del nombre.
Moltes vegades quant es parla de calcular un nombre irracional, per exemple el nombre o el nombre π el que es vol dir és trobar un algorisme que vagi donant els diferents dígits de la seva representació decimal tot i que com que el nombre no és racional aquests dígits ni s'acabaran mai ni arribaran a un bucle que es repeteixi, i per tant aquest algorisme no s'acabarà mai.
Fixeu-vos que aquesta successió no és tan forta com la fracció irreductible dels racionals perquè depèn de la base que s'escolleixi per representar els nombres, si en comptes de la base 10 s'escull la base 2 llavors surt una successió completament diferent, a demés i depenent també de la base, hi ha nombres que tenen dues successions que els representen, per exemple:
És fàcil veure que efectivament aquestes dues successions representen el mateix nombre perquè en calcular la successió diferència surt:
Que es veu clar que tendeix cap a zero perquè per a qualsevol nombre per petit que sigui sempre es pot trobar un nombre a partir del qual els termes de la successió són tots més petits.
Extensió de la suma Un cop identificats els nombres reals amb els límits de les successions de Cauchy llavors es poden estendre les operacions en els nombres racionals als nombres reals de la següent forma:
La recta real
[modifica]La recta real permet una relació entre una recta de l’espai físic i el conjunt dels nombres rals, i així visualitzar el conjunt dels nombres reals com els punts d’una recta de l’espai.
Es considera una recta R que conté un punt O que es diu, per convenció, origen i que s'identifica amb el nombre 0. S’agafa un punt l diferent d'O que pertany a R i s'identifica al nombre 1. Es diu que la distància d'O a l és igual a 1 (això és arbitrari i correspon a l’establiment de la unitat de mesura de longitud de l’espai físic) i que l'orientació de la recta és la que va d'O cap a l. A tot punt M de la recta, se li associa la distància entre O i M (prenent la distància entre O i l com a unitat de mesura de distàncies). Si el M i I són al mateix costat respecte de O llavors la distància es considera positiva, si no negativa.
Aquesta relació, que la formalització actual en diu bijecció permet identificar cada nombre real amb un punt d'una recta.

A la recta real es representen tots els nombres reals, per tant s'hi poden identificar cada un dels conjunts de nombres naturals, enters i racionals si s'identifiquen com a subconjunts dels nombres reals.
A base d'anar repetint distàncies iguals a la distància entre el punt O i el punt l cap a la dreta i contant s'identifiquen els nombres reals 2,3,..., si aquestes distàncies s'ubiquen cap a l'esquerra del punt O llavors els punts de la recta s'identifiquen amb els punts -1, -2, ... Fixeu-vos que el fet de triar que els positius vagin cap a la dreta i els negatius cap a l'esquerra és purament convencional i es podria haver fet exactament a l'inrevés.
Dividint en deu parts iguals el segment entre dos punts identificats amb dos nombres naturals s'obtenen punts identificats amb nombres que tenen un nombre enter m-es unes dècimes, dividint entre deu parts iguals els punts identificats amb les dècimes s'obtenen punts identificats amb centèssimes:

Per dividir un segment entre un nombre determinat de parts iguals es fan servir tècniques que s'estudiaran en l'apartat de geometria.
Ordenació
[modifica]Es diu que un conjunt està totalment ordenat si es pot establir entre els seus elements una relació d'ordre total. Una relació d'ordre es pot entendre com una operació que aplicada a dos nombres x i y s'escriu x≤y i només pot donar dos resultats cert o fals i que compleix les següents propietats:
- Propietat reflexiva: x ≤ x per a tot x de R
- Propietat transitiva: si x ≤ y i y ≤ z llavors x ≤ z
- Propietat antisimètrica: si x ≤ y i y ≤ x llavors x = y
- Ordre total: per a tot parell x, y de R, o bé x ≤ y o bé y ≤ x
La relació x ≤ y es llegeix x és més petit o igual que y o també y és més gran o igual que x i també es pot escriure y ≥ x totes dues notacions i totes dues expressions volen dir exactament el mateix. Si x ≤ y però x no és igual a y llavors també es diu que x és més petit que y o que x és estrictament més petit que y.
Es tracta de definir una relació en el conjunt dels nombres reals que complexi aquestes propietats i que porti al resultat natural de que a la recta real els punts que estan més a l'esquerra siguin més petits que els que estan més a la dreta. La idea és restar-los i si el resultat és positiu dir que el minuend és més gran que el subtrahend per això cal definir els nombres positius, però sense fer servi l'expressió més gran o igual que zero (perquè encara no s'ha acabat de definir la relació d'ordre i no es pot parlar amb propietat de més gran que en el conjunt dels nombres reals). La solució és basar-se en la relació d'ordre que ja existeix en els nombres racionals i a partir d'aquí definir el concepte de nombre positiu en els reals:
Un nombre real x és positiu si, o bé és zero, o bé existeix un nombre racional ε tal que si an és una successió de Cauchy de nombres racionals que tendeix a x, existeix un N0 tal que per a tot n > N0 es compleix que an > ε.
Llavors es defineix la relació d'ordre dient que x ≤ y si i només si x - y és positiu.
Valor absolut
[modifica]Es diu valor absolut d'un nombre real x i s'escriu |x| al mateix nombre si és positiu i al nombre multiplicat per -1 si és negatiu:
Propietats dels nombres reals
[modifica]Totes les successions de Cauchy en el conjunt dels nombres reals tenen límit.
Això seria el paral·lel a veure que el conjunt dels nombres reals és tancat vers la operació de trobar el límit de les successions de Caucy d'aquesta propietat se'n diu completesa i el fet que R la tingui es diuu que R és complet. Igual que en el cas dels nombres racionals són tancats vers la operació de dividir, recordeu que la divisió de dos enters, per definició és un racional però cal comprovar que la divisió de dos racionals també és una racional.
Aquesta afirmació sembla clara però cal analitzar-la amb detall. Totes les successions de Cauchy de nombres racionals tenen límit en un nombre real (racional o no) ja que la pròpia successió és per definició un representant del nombre real. Però que passa si la successió és de nombres reals. Per poder afirmar que té límit real cal veure que es pot construir una successió de nombres racionals que té el mateix límit.
Una successió de nombres reals de fet és una successió de successions (cada nombre real és una successió)
(inacabat)
Tota successió creixent i fitada superiorment té límit
Per veure que una successió creixent i fitada superiorment te límit en els reals n'hi ha prou amb veure que és de Cauchy (llavors per la completesa dels reals la successió ha de tenir límit). Fixeu-vos que passaria si no fos de Cauchy: hi hauria pel capbaix un ε >0 tal que per tot N0 (per tant es comença amb 1) es podrien trobar n i m més grans que N0=1 tals que an - am > ε. Com que la successió és creixent ha de ser an > a1 + ε. Ara es pot repetir el procés agafant un N1 > n i trobar n' i m' estiguin separats més que ε, llavors an' > a1 + 2ε i així sucessivament. Això és una contradicció si la successió és fitada. Si la fita és f només cal repetir el procés més de (f - a1)/ ε vegades per trobar un terme de la successió més gran que la fita.
Intervals en el conjunt dels nombres reals
Un interval és un subconjunt del conjunt dels nombres reals caracteritzat perquè si dos nombres pertanyen al subconjunt tots els que estan entremig també. Si a i b pertanyen al subconjunt i c és tal que, per exemple a < c < b llavors c també pertany al subconjunt. Alguns autors inclouen el conjunt buit com un interval: l’interval buit. Si un interval consta d’un únic punt es diu que és un interval degenerat.
Si hi ha un nombre a tal que els punts x < a no pertanyen a l’interval llavors es diu que l’interval és fitat inferiorment.
Si hi ha un punt b tal que els punts x > b0 no pertanyen a l’interval llavors es diu que l’interval és fitat superiorment.
Si un interval fitat inferiorment té una fita inferior que pertany a l'interval llavors es diu que l'interval és tancat en l'extrem esquerre. Si no hi ha cap fita inferior que pertanyi a l'interval llavors es diu que és obert per l'extrem esquerre. Fixeu-vos que els intervals no fitats inferiorment són oberts per l'extrem esquerre.
Si un interval fitat superiorment té una fita superior que pertany a l'interval llavors es diu que l'interval és tancat en l'extrem dret. Si no hi ha cap fita superior que pertanyi a l'interval llavors es diu que és obert per l'extrem dret. Fixeu-vos que els intervals no fitats superiorment són oberts per l'extrem dret.
Si un interval és tancat pels dos extrems es diu simplement que és tancat. Si és obert pels dos extrems es diu que és obert.
Tot seguit es resumeixen els diferents tipus d'intervals i es dóna la seva notació:
En resum, es fa servir un parèntesi "(" per indicar que l'interval és obert i un claudàtor "[" per indicar que és tancat, tot seguit s'escriu la més gran de les fites inferiors si l'interval és fitat inferiorment o el símbol "-∝" si no ho és, a continuació s'escriu una coma "," i la més petita de les fites superiors si l'interval és fitat superiorment o el símbol "∝" si no ho és i per acabar un parèntesi ")" per si l'interval és obert superiorment o un claudàtor "]" si és tancat.
Quants nombres reals hi ha?
En el cas dels nombres racionals s'ha vist que es podien contar, és a dir que es podien posar en relació amb els nombres naturals de forma que a cada nombre racional li correspongués un i només un nombre natural. Això dóna una idea de que la quantitat infinita de nombres racionals és exactament igual de gran que la quantitat infinita de nombres naturals. Per veure-ho n'hi ha hagut prou amb presentar una manera de construir aquesta relació, una manera de contar els nombres racionals.
En el cas dels nombres reals resulta que això no es pot fer, no es poden contar. Per veure-ho caldrà veure que qualsevol de les possibles maneres de contar nombres reals sempre en deixa algun a fora.
La idea de la demostració té dues etapes, primer es tracta d'agafar una successió qualsevol de nombres reals an (Contar nombres reals és construir una successió). Llavors a partir d'aquesta successió qualsevol es construeix una successió d'intervals tancats tals que cada un està completament contingut en els anteriors i no n'hi ha cap de buit. A demés questa successió d'intervals tancats es construeix de tal manera que l'interval n no contingui cap dels n+2 primers nombres reals de la successió an.
El primer interval es construeix agafant els dos primers nombres reals de la successió a1 i a2. Per tal que no hi siguin, es calculen els nombres b1=(a1 + a2) / 3 i c1=2•(a1 + a2) / 3. El primer interval de la successió I 1 és l'lnterval tancat limitat per aquests dos nombres: [b1,c1]. Queda clar que l'interval no és buit i que els dos primers nombres de la successió no hi són dins. A partir d'aquí es van construint els següents intervals. Si els nombre an+2 queda fora de l'interval I n llavors no es toca res i l'interval I n+1 continua sent el mateix, és a dir I n+1 = I n. En canvi si el nombre an+2 està dins de l'interval llavors es retalla l'interval de forma que se'n obtingui un altre de tancat i no buit però que deixi aquest nombre fora, per exemple si an+2 està més a prop de bn que de cn llavors es calcula el nou bn+1= (an+2 + cn)/3. Si el que està més a prop de an+2 és el cn llavors el que es canvia és el cn+1 = 2•(bn + an+2)/3.
Fixeu-vos que això també es pot fer amb els nombres racionals, per tant la part important de la demostració ve ara. Es tracta de veure que en el conjunt dels nombres reals existeix pel capbaix un nombre que pertany a tots els infinits intervals que es generen amb la successió, per tant un nombre que no surt mai a la successió. Com que això es pot fer amb qualsevol successió llavors resulta impossible comptat tots els nombres, totes les formes possibles de intentar contar-los sempre es deixen nombres sense contar.
Si es té una successió infinita d'intervals tancats i encaixats es pot construir una successió de nombres agafant la successió que s genera per exemple pels extrems inferiors de l'interval. Aquesta successió és creixent i mai no passa de c1 per tant té límit l el límit és a dins de tots els intervals (perquè és més gran que tots els extrems inferiors i és més petit que tots els extrems superiors). Per tant, pel capbaix existeix un nombre real l que pertany a tots els intervals.
Fixeu-vos que en el cas dels nombres racionals no sempre existeix aquest límit una successió de nombres racionals pot donar un nombre irracional com ja s'ha vist en exemples anteriors.
Encara no hem acabat de contestat la pregunta, ara sabem que no es poden contar tots els nombres reals perquè sempre en queda algun fora, per tant n'hi ha més que no pas naturals, però quants més, potser només uns quants? El fet és que n'hi ha d'haver molts més que no pas racionals. Fixeu-vos que si la quantitat de nombres que no són racionals fos numerable llavors com que els racionals ho són es podrien assignar els racionals als nombres parells i els irracionals als senars i s'haurien contat tots els reals. El fet que els reals no siguin numerables vol dir que els irracionals tampoc ho són i per tant n'hi ha molts més que no pas racionals.
Estimació i aproximació de quantitats
[modifica]Els nombres que s'han estudiat fins aquí pertanyen tots a conjunts infinits. Alguns com els nombres naturals petits es poden representar en la memòria d'un ordinador o una calculadora o es poden escriure en un paper emprant sistemes de numeració com ara base 10 o base 2 o números romans. Però no hi ha cap sistema capaç d'escriure o emmagatzemar qualsevol nombre natural pel senzill motiu que hi ha nombres prou grans que no hi caben a cap sistema. En el cas dels nombres racionals en la seva representació decimal la situació és més complicada perquè el bucle de xifres abans de repetir-se pot ser tant llarg com el denominador de la fracció irreductible, per exemple en el cas de 1/17 té 16 xifres (fixeu-vos que per emmagatzemar el numerador i el denominador amb 3 xifres n'hi ha prou), hi hauria la possibilitat d'emmagatzemar-los en forma de fraccions però resulta que fraccions que representen nombres relativament petits poden necessitar nombres molt grans per ser representades per exemple 100.000.000/100.000.001 és pràcticament igual a 1 però necessita dos nombres de 15 xifres cada un. En el cas dels nombres irracionals la cosa es complica encara més la seva representació decimal no es repeteix mai i no hi ha cap sistema d'emmagatzemament de dades que pugui contenir la representació decimal d'un sol nombre irracional. En alguns nombres irracionals es pot plantejar de emmagatzemar la cadena d'operacions o l'algorisme que porta a definir el nombre (per exemple emmagatzemar ) això és molt interessant i hi ha programes que ho fan tot i que són molt complexos, els nombres reals que es poden obtenir d'aquesta manera són no obstant mot pocs comparats amb tots els que hi ha. Fixat que els nombres irracionals no són numerables i els nombres que es poden representar així si que ho són.
Independentment de les limitacions i de les dificultats per emmagatzemar la representació decimal d'un nombre en les aplicacions pràctiques en física, enginyeria i economia, poques vegades té sentit fer servir gaires xifres per representar un nombre: Els instruments de mesura tenen una precisió limitada i a partir d'una certa xifra de la representació decimal, el valor llegit a l'instrument és incert. Les unitats monetàries es fan servir amb un nombre de xifres decimals limitat i definit per la llei.
Tots aquests motius porten a la necessitat d'emprar valors aproximats per a representar quantitats.
Truncament i arrodoniment
[modifica]El truncamiento redondeo son métodos para aproximar cantidades reduciendo el número de dígitos de su representación. Al basarse en la reducción del número de dígitos tienen cierta dependencia de la base del sistema de numeración empleado.
Los sistemas de redondeo y truncamiento vienen a responder a la pregunta siguiente: se conoce una magnitud con un determinado númeronde dígitos en su representación decimal (también puede ser binaria, octal etcétera). ¿Por qué número hay que aproximar esta cantidad si se quiere emplear sólomdígitos conm<n?
Una posible respuesta es depreciar los dígitos que aportan menos cantidad a la magnitud. Como los dígitos de más a la izquierda representan partes más grandes se deprecian los de más a la derecha. De este método se llamatruncamiento por defecto y de la posición de la cifra cifra menos significativa que se conserva se llamaorden de la aproximación, por ejemplo si se tiene el número 1234.567 y se quiere truncar por defecto con el orden de las decenas resulta 1230 (un número entero de decenas). Si la aproximación se quisiera del orden de la décima el truncamiento por defecto daría 1234,5
En truncar por defecto el número aproximado difiere del original en una cantidad que va de 0 hasta la décima (en caso de que el orden de la aproximación sea la décima). Esta diferencia se llamaerror'. Tenga en cuenta que al truncar hacia abajo el error es siempre mayor que cero.
De hecho el número 1234.567 se encuentra en medio del 1230 y el 1240, si se trata de aproximarse por un número que sólo tenga dígitos hasta las decenas. No hay ningún motivo para preferir a uno en lugar del otro, de hecho en este caso está más cerca de 1230, pero en el caso de la aproximación del orden de la décima el número está más cerca de 1.234,6. Del hecho de aproximarlo por 1,240 (es decir la décima inmediatamente superior) se llamatruncamiento por exceso. En este caso el error es siempre negativo.
Como a veces el número está más cerca del resultado del truncamiento por defecto y otras veces lo está más del truncamiento por exceso parece una buena idea elegir cada vez aquel que dé un error de módulo más pequeño, de este tipo de aproximación se 'n dice redondeo. Para ello lo único que hay que pactar es que se hace en el caso de que esté exactamente a la misma distancia de ambos, por ejemplo en aproximar el número 123.5 para obtener una aproximación del orden de las unidades. En este caso la convención más práctica y la que se toma es el truncamiento por exceso y este número se redondea a 124. Al tomar esta convención facilita los algoritmos de redondeo porque sólo hay que mirar la primera cifra a depreciarse para decidir qué tipo de truncamiento hay que hacer, el número 123,5 redondea al igual que el número 123.5000000000001. En caso de aproximación por redondeo a veces el error es positivo ya veces es negativo.
Errors
[modifica]Ja s'ha comentat que en aproximar un nombre es comet un error: la diferència entre el nombre i la seva aproximació. D'aquest error de vegades també se'n diu error absolut i es nota com Ea
En el cas d'aproximar nombres racionals de vegades aquest error es pot calcular amb exactitud (si el nombre hi cap a la memòria) però de vegades no, en el cas de nombres irracionals l'error no es pot calcular i representar com un nombre decimal. En aquests casos es pot trobar una fita de l'error, per exemple, si s'aproxima el nombre pel nombre 1,41 es comet un error més petit de 0,005 perquè , per tant ,005 és una fita de l'error absolut d'aquesta aproximació.
El fet de cometre un error de 0,005 metres (5 mil·límetres) en una magnitud de l'ordre de 1,4 metres no té la mateixa importància que cometre aquest mateix error en la mesura d'una magnitud de 0,01 métres (10 mil·límetres) en el segon cas l'error és gairebé tan gran com la magnitud. Per tenir una quantificació més clara de la importància de l'error respecte de la magnitud es defineix l'error relatiu com el quocient entre l'error i la magnitud i es nota com Er. Així en el primer cas l'error relatiu és de:
mentre que en el segon cas és de:
L'error relatiu també es pot expressar en percentatge. El percentatge d'error és 100·Er.
En els casos en què el que es coneix és una fita de l'error absolut també es defineix la corresponent fita de l'error relatiu.
Errors i operacions aritmètiques
Per entendre l'impacte de l'error en les operacions aritmètiques es planteja un exemple, hi ha dos nombres que s'han arrodonit a la unitat i per tant la seva representació té error:
Fixeu-vos que en aquest cas les xifres significatives han desaparegut i tot el resultat ha quedat contingut a l'error. Sempre que es resten dos nombres molt semblants el valor absolut del resultat es fa més petit i l'error és de l'ordre de la suma d'errors, per tant l'error relatiu es fa molt més gran. D'aquest fenomen se'n diu cancel·lació catastròfica i tots els algorismes informàtics que empren nombres aproximats l'han de tenir en compte en fer les operacions aritmètiques, de vegades els algorismes s'han de fer més complicats del que resultaria d'aplicar directament les fórmules per evitar que aparegui aquest fenomen.
Potències i arrels
[modifica]Igual com s'han estès les operacions de sumar, restar multiplicar i dividir dels nombres racionals als nombres reals es pot estendre la potenciació de la següent forma:
On el cantó esquerra de la igualtat representa el terme genèric d'una successió que tendeix a ab i la banda dreta explica que aquesta successió es construeix agafant dues successions de nombres racionals an i bn que tinguin per límits respectivament a i b i construint una nova successió a base d'elevar cada un dels termes an al corresponent terme bn. Com que la potenciació en els racionals ja està definida, aquesta nova successió es pot calcular.
Llavors la potenciació en els reals hereta totes les propietats de la potenciació en els naturals, enters i racionals. Tot seguit es presenta un resum d'aquestes propietats que ja s'han explicat en els respectius apartats:
Notació científica. Operacions amb notació científica
[modifica]Logaritmes
[modifica]L'operació de potenciació relaciona tres nombres a, b i c de forma que ab = c. Per tant hi ha dos punts de vista per plantejar l'operació inversa: donats a i c trobar b o donats b i c trobar a. el segon cas és la mateixa potenciació però a l'exponent invers:
En canvi en el primer cas apareix una operació nova que es diu logaritme en base a, es diu que b és el logaritme en base a de c si ab = c i s'escriu tal com segueix:
Logaritmes decimals
[modifica]El logaritme en base 10 s'anomena logaritme decimal i es representa com a , sense cap tipus de base.
Exemples de logaritmes en base 10:
Logaritmes neperians
[modifica]Hi ha un tipus de problemes que es poden resoldre emprant logaritmes, per exemple: Una conilla al cap d'un mes d'haver nascut ja és adulta i al cap d'un més més ja té 10 cries, 5 mascles i 5 femelles, llavors cada dos mesos torna a criar. Quants anys caldrien perquè tota la massa de la terra fos carn de conill?
El primer que cal veure és per quant es multiplica cada any el nombre de conilles. Encara que la conilla inicial es reprodueix a un ritme anual de 31 (5 cries cada 2 mesos més ella mateixa = 1+5·6=31) com que les cries també crien, el resultat és que el nombre de conilles es multiplica per 6 = 1+5 sis cops a l'any (cada 2 mesos) per tant cada any el nombre de conilles es multiplica per 66=46.656. Com que la massa de la terra és de 5.973.000.000.000.000.000.000.000 kg i cada conill fa aproximadament 1 kg es tracta de saber els anys que trigarà la conilla inicial en multiplicar-se per 2.986.500.000.000.000.000.000.000 (la meitat de la massa de la terra ja que al final hi haurà també aquest nombre de mascles). Per tant es tracta de trobar:
És a dir que això passarà pràcticament d'aquí a 5 anys i 3 mesos.
Fixeu-vos que s'ha hagut de trobar per quant es multiplica cada unitat de temps (cada any) el nombre de conills a partir de saber a quin ritme anual es multiplica la conilla inicial. Ha resultat que, tot i que una conilla es multiplica a un ritme de 31 cada any (5 cries cada dos mesos més ella mateixa), com que les cries també tenen cries l'efecte total és de multiplicar-se per 46.656.
Observeu que passaria amb un animal que també es multipliqués a un rítme anual de 31 però que en comptes de criar 6 cops a l'any criés 3 cops a l'any (és a dir cada 4 mesos), en aquest cas el factor pel que es multiplicaria la població cada unitat de temps (cada any) seria:
A la natura hi ha fenòmens que es pot assimilar a com si es reproduïssin infinites vegades en una unitat de temps, per exemple la desintegració radioactiva. Cada nanosegon en un volum de material radioactiu hi ha una determinada quantitat de material que es desintegra i aquest material ja no està disponible per desintegrar-se al nansegon següent. O en una explosió nuclear els neutrons triguen nanosegons en xocar contra nous nuclis i multiplicar-se. La reproducció dels microorganismes es produeix una quantiat enorme de vegades cada any...
En aquest fenòmens el factor pel qual es multipliquen cada unitat de temps és:
on k és el rítme a que "cria" una unitat en una unitat de temps. Tots aquests factors es poden trobar a partir de conèixer el factor d'un fenomen que "crii" a un rítme de 1 (és a dir que es reprodueixi a un rítme de multiplicar-se per 2 cada unitat de temps:
Aquest nombre s'anomena nombre e.
El cas anterior es pot calcular a partir del nombre e perquè es compleix el següent:
La demostració es farà pel cas de k natural (els casos enter, racional i real sorgeixen aplicant les propietats de les potències i les successions). Una forma de demostrar que una propietat es compleix per a tots els nombres naturals és el que s'anomena demostració per inducció completa el que es fa és demostrar primer que es compleix per zero, llavors se suposa que es compleix per a tots els nombres naturals més petits o iguals que k i es demostra que també s'ha de complir per a k + 1. Fixeu-vos que el que s'està fent és trobar un mecanisme que a partir del zero, a base de repetir el procés tants cops com calgui permet demostrar que la propietat es compleix per a qualsevol nombre m per gran que sigui m.
Fixeu-vos que pel cas de k = 0 la propietat es compleix perquè:
i
Tot seguit es calcula per k+1 suposant que la propietat es compleix per tots els valors fins a k.
Si aquest nombre real és igual a ek+1 llavors la propietat ja està demostrada. Recordeu que dues successions representen el mateix nombre real si la seva diferència tendeix a zero, tot seguit es calcula:
Fixeu-vos que quan n és més gran que k+1 el resultat de (k+1)/n és més petit que 1 i elevat a n és encara més petit, però sempre positiu. Per tant, és evident que els termes de la successió s'apropen tant com és vulgui a zero, és a dir el límit d'aquesta successió és zero.
Dons bé, es defineix el logaritme neperià d'un nombre com el logaritme en base e i s'escriu ln:
per tant:
Propietats i aplicacions
[modifica]Els logaritmes tenen propietats que precedeixen de les propietats de la potenciació. A la següent taula es presenten les que fan referència al logaritme del producte quocient, potència i arrel amb la corresponent demostració.
Per a les demostracions se suposa que:
| Propietat | Demostració |
|---|---|
|
| |
|
| |
|
| |
|
|
Fixeu-vos que aquestes propietats fan que els logaritmes transformin el problema de multiplicar i dividir en un problema de sumar i restar i els problema de elevar a una potència i extreure una arrel en el problema de multiplicar i dividir. Antigament es feien servir els logaritmes per resoldre aquests càlculs. El procediment era el següent:
Per multiplicar (o dividir) dos nombres:
- Emprant la taula de logaritmes, trobar el logaritme de cada nombre
- Sumar els dos logaritmes (o restar-los)
- Emprant la taula, trobar l'antilogaritme (la inversa del logaritme, que de fet és la potència) del resultat.
Per elevar un nombre x a una potència y (o extreure una arrel y de x)
- Emprant la taula de logaritmes, trobar el logaritme de x
- Multiplicar el logaritme de x per y (o dividir-lo entre y)
- Emprant la taula trobar l'antilogaritme del resultat.
Aquesta idea permet construir un enginy per fer càlculs molt fàcilment, si es construeix un conjunt de regles que poden lliscar entre ells i les distàncies en comptes de ser proporcionals als nombres que hi estan escrits ho són als seus logaritmes, posar un nombre al costat d'un altre (sumar els logaritmes) permet llegir en un tercer regle directament el producte, o acumulant diverses vegades una longitud permet llegir en un segon regle la potència i així.

A demés de les propietats anteriors a partir de la definció de logaritme es poden deduir les propietats que permeten calcular l'antilogaritme (la inversa del logaritme) i el canvi de base (conèixer el logaritme en bade b d'un nombre a partir de conèixer el logaritme en base a d'aquest nombre).
A partir de:
Es dedueix:
| Propietat | Demostració |
|---|---|
|
| |
|
|
























![{\displaystyle (-a)+(-b)+a+b=[a+(-a)]+[b+(-b)]=0+0=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d96405282c8ab68019b884960de410f5b1928a2a)

![{\displaystyle a+(-b)=a+(-b)+b-b=a+[(-b)+b]-b=a-b\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ec52cb6ae2993bbc4f68531ebe02304ab037ee6)













![{\displaystyle {\frac {a}{b}}+\left[-\left({\frac {a}{b}}\right)\right]={\frac {a}{b}}+{\frac {-a}{b}}={\frac {a-a}{b}}={\frac {0}{b}}={\frac {0}{1}}=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94fd86eb1bb76f1837d094940fb1ef7beda06105)


















![{\displaystyle {\sqrt[{m}]{a^{m\cdot n}}}=a^{n}=a^{\frac {m\cdot n}{m}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/575bad1f4af2efea43d034aa970e4043f8e38586)
![{\displaystyle a^{\frac {b}{c}}={\sqrt[{c}]{a^{b}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98e4cda1f8eb5526efa885afa97dd5db0506aad9)




























































![{\displaystyle {\begin{aligned}&x^{-y}={\frac {1}{x^{y}}}\\&x^{{y}/{z}\;}={\sqrt[{z}]{x^{y}}}\\&x^{-{y}/{z}\;}={\frac {1}{\sqrt[{z}]{x^{y}}}}\\&x^{y}\cdot x^{z}=x^{y+z}\\&{\frac {x^{y}}{x^{z}}}=x^{y-z}\\&\left(x^{y}\right)^{z}=x^{y\cdot z}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed7c30884fc0a4f0a8315a8ee9cc308bdc65e6d6)
![{\displaystyle {\begin{aligned}&a^{b}=c\\&a={\sqrt[{b}]{a^{b}}}={\sqrt[{b}]{c}}=c^{{1}/{b}\;}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d99ec32a8ab9b2fb7392e627ba7a165e8b809b0)











![{\displaystyle {\begin{aligned}e^{k+1}&=e\cdot e^{k}\\&={\underset {n\to \infty }{\mathop {\lim } }}\,\left(1+{\frac {1}{n}}\right)^{n}\cdot {\underset {n\to \infty }{\mathop {\lim } }}\,\left(1+{\frac {k}{n}}\right)^{n}\\&={\underset {n\to \infty }{\mathop {\lim } }}\,\left[\left(1+{\frac {1}{n}}\right)\cdot \left(1+{\frac {k}{n}}\right)\right]^{n}\\&={\underset {n\to \infty }{\mathop {\lim } }}\,\left(1+{\frac {1}{n}}+{\frac {k}{n}}+{\frac {k}{n^{2}}}\right)^{n}\\&={\underset {n\to \infty }{\mathop {\lim } }}\,\left(1+{\frac {k+1}{n}}+{\frac {k}{n^{2}}}\right)^{n}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce84f1288feddc1663c64640938e321283dbf0e6)










![{\displaystyle \log _{x}\left({\sqrt[{b}]{a}}\right)={\frac {\log _{x}\left(a\right)}{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1caac54719b105deb903120e0596a191f8c2f4e)
![{\displaystyle {\begin{aligned}\log _{x}\left({\sqrt[{b}]{a}}\right)&=\log _{x}\left({\sqrt[{b}]{x^{y}}}\right)\\&=\log _{x}\left(x^{{y}/{b}\;}\right)\\&={\frac {y}{b}}\\&={\frac {\log _{x}\left(a\right)}{b}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acd63d9efefe89840d0fa3e5cff5c984ea0009b1)




