Operacions amb nombres naturals
La suma
[modifica]Intuïtivament la suma de nombres naturals es pot definir de la següent manera:
Siguin a i b dos nombres naturals i siguin A i B dos conjunts amb a i b elements respectivament (és a dir tals que el cardinal(A) = a i cardinal(B) = b) llavors es diu que el nombre natural c és igual a la suma de a i b i s'escriu c = a + b si i només si c = cardinal(A ∪ B) (és a dir si c és el nombre d'elements del conjunt unió de A i B).
Si els nombres naturals s'han definit a partir dels axiomes de Peano llavors la suma es defineix amb l'expressió:
a + (b + 1) = (a + b) + 1
on + 1 s'ha d'entendre com l'operació següent de dels axiomes de Peano, per tant aplicant successivament la definició fins que només quedin operacions de suma 1, el nombre natural resultat de la suma queda determinat.

Propietats de la suma
[modifica]- Propietat commutativa: la suma no varia en canviar l'ordre dels seus sumands.
- a + b = b + a

- Propietat associativa: el resultat de la suma és independent de la forma en què s'agrupen els sumands.
- (a + b) + c = a + (b + c)
Si s'interpreta la suma com comptar els elements de la unió de conjunts és fàcil veure intuïtivament que aquestes propietats s'han de complir. Emprant els axiomes de Peano, el resultat és el mateix perquè, de fet, la definició de sumà es pot entendre com que a partir del primer nombre es compta (següent de) tantes vegades com indica el segon. Llavors arribar a la concussió de què es copleixen la propietat commutativa i associativa és qüestió de plantejar una demostració per inducció.
Algorisme de sumar
[modifica]| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|
| 2 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 4 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| 5 | 10 | 11 | 12 | 13 | 14 | |||
| 6 | 12 | 13 | 14 | 15 | ||||
| 7 | 14 | 15 | 16 | |||||
| 8 | 16 | 17 | ||||||
| 9 | 18 |
Una algorisme per sumar és un algorisme que a partir de l'expressió dels nombres que es vol sumar dóna l'expressió del nombre resultat de la suma. Emprant la definició de suma això es podria fer comptant a partir del primer nombre una quantitat de vegades igual al segon nombre. Però això requereix un nombre d'operacions igual al segon nombre.
Si els nombres s'escriuen emprant un sistema de numeració posicional l'algorisme de trobar l'expressió del nombre resultat d'altres dos es pot realitzar amb un nombre d'operacions igual al nombre de xifres de la representació dels nombres. Per tant proporcional al logaritme dels nombres.
Per aplicar l'algorisme de sumar primer cal una taula amb el resultat de sumar totes les possibles parelles de nombres d'una xifra. En cas de nombres en base 10, 10 × 10 = 100 parelles. Aprofitant la propietat commutativa es pot reduir a la meitat i aprofitant que el zero és l'element neutre de la suma es poden estalviar 10 parelles i aprofitant que sumar 1 és comptar el següent per tant en queden 36.
Llavors es procedeix tal com s'explica a continuació:
- S'escriuen els nos nombres un damunt de l'altre ficant en columnes alineades les unitats, les desenes, centenes etc. I es traça una ratlla al davall. A l'esquerra del segon nombre s'escriu una creu per indicar que l'operació a realitzar és una suma.
- Es busca a la taula el resultat de sumar les xifres de les unitats (o es recorda de memòria). Si el resultat és més petit que 10 s'escriu davall de la ratlla a la columna de les unitats. Si és més gran o igual a 10 s'escriu davall de la ratlla a la columna de les unitats la primera xifra del resultat i s'escriu un 1 al damunt de la columna de les desenes.
- Es busca a la taula el resultat de sumar les xifres de les desenes i si hi ha un 1 al damunt de la columna s'afegeix una unitat més. Llavors amb el resultat obtingut es procedeix igual que en el cas de les unitats però desplaçat una columna.
- Es repeteix el procés fins que s'acabin les columnes. Llavors el nombre que apareix davall de la ratlla és el resultat de sumar els altres dos.
Exemple:
11 1 348.493 + 47.692 -------- =396.185
Per demostrar que aquest algorisme dóna el resultat correcte cal aplicar la propietat distributiva de la suma i la multiplicació i es veurà després de la multiplicació.
La resta
[modifica]La resta és l'operació inversa de la suma. És a dir es diu que un nombre c és igual a a - b si c + b = a. Per tant l'operació de restar de a el nombre b és trobar un nombre c tal que sumat a b doni a.
Restar és llevar o suprimir, és a dir, calcular la diferència.
La resta s'expressa de la manera següent: a − b = c, on a s'anomena minuend, b s'anomena subtrahend i c és el resultat de la resta o diferència.
En el conjunt dels nombres naturals, N, només es poden restar dos nombres si el minuend és major o igual que el subtrahend. Si el minuend i el subtrahend són iguals, la diferència és zero. Per això es diu que el conjunt dels nombres naturals no és tancat respecte de la resta, perquè donats dos nombres naturals qualsevol a i b no sempre existeix un nombre natural c tal que c = a - b.
Propietats de la resta
[modifica]L'operació de restar té les següents propietats:
- Uniforme: Si als dos membres d'una igualtat se'ls resta un mateix nombre, queda una altra igualtat com a resultat.
a = b ⇒ a − c = b − c
- Monotonia : Si als dos membres d'una desigualtat matemàtica se'ls resta un mateix nombre, queda una altra desigualtat del mateix sentit.
a > b ⇒ a − c > b − c
Algorisme de restar
[modifica]Seria possible restar dos nombres a base de comptar enrere a partir del minuend tantes vegades com unitats té el subtrahend, però aquest algorisme requereix tantes operacions com unitats té el subtrahend. Si els nombres que s'han de restar estan escrits en un sistema de numeració posicional, es pot obtenir el resultat amb un algorisme que només necessita tantes operacions com xifres cal per representar els nombres, és a dir un nombre d'operacions proporcional al logaritme dels nombres.
Per aplicar l'algorisme de la resta es pot emprar la mateixa taula que es fa servir per l'algorisme de la suma o memoritzar-la. La taula cal llegir-la en sentit invers, per exemple per trobar el nombre que cal sumar a 5 perquè doni 13 (restar 5 de 13) es busca el nombre 13 a la columna o a la fina del 5, en aquest cas es troba que el 13 està a la fina del 5, llavors el resultat de restar 5 de 13 és el nombre que hi ha a la capçalera de la columna on s'ha trobat el 13 per tant és 8. Per exemple per restar 9 de 16, el 16 està a la columna del 9 per tant el resultat és el nombre que hi ha a la capçalera de la fila del 16: 7.
Aquesta taula només serveix per a restar nombres d'una xifra a minuends tals que el resultat doni un nombre també d'una xifra. Llavors per restar nombres de diverses xifres, es procedeix de a següent manera:
- S'escriuen els nos nombres un damunt de l'altre ficant en columnes alineades les unitats, les desenes, centenes etc. I es traça una ratlla al davall. A l'esquerra del subtrahend s'escriu un guió per indicar que l'operació a realitzar és una resta.
- Si la xifra de les unitats del minuend és més gran o igual que la xifra de les unitats del subtrahend , es busca a la taula el resultat de restar les xifres de les unitats (o es recorda de memòria) i el resultat s'escriu davall de la ratlla a la columna de les unitats. Si la xifra de les unitats del minuend és més petita que la xifra de les unitats del subtrahend llavors s'afegeix una desena a la xifra de les unitats del minuend i es procedeix de la mateixa manera. El fet d'haver afegit una desena a les unitats cal compensar-ho més endavant al restar les desenes, d'això, que cal memoritzar-ho, se'n diu portada.
- Llavors es continua de la mateixa manera amb les desenes, però si a les unitats ha calgut afegir-hi una desena al minuend ara cal compensar-ho restant una desena més que les que indica el subtrahend. Aquest fet es recorda de memòria i es procedeix afegint la portada al subtrahend.
- Es repeteix el procés fins que s'acabin les columnes. Llavors el nombre que apareix davall de la ratlla és el resultat de restar del minuend el subtrahend.
Exemple:
348.493 - 47.692 -------- =300.801
Fixeu-vos que al restar les xifres de les centenes ha calgut afegir 10 al 4 per obtenir 14 - 6 = 8 que és la xifra de les centenes del resultat. Llavors s'ha afegit la portada a la xifra dels milers dels subtrahend ( 7 + 1 = 8) i s'ha continuat fent 8 - 8 = 0 que és la xifra dels milers del resultat.
Aquest algorisme és idèntic al que explica Francesc Santcliment a la seva obra Suma de la art de Arismètica 1482, un dels primers llibres de matemàtiques que es va imprimir a Europa en aparèixer la impremta
[1] i és el que normalment s'explica a les escoles als Països Catalans. Una variant és escrivint la portada com un superíndex a la xifra del subtrahend de forma que no cal confiar en la memòria. En altres països [2] s'ensenya l'algorisme de "prendre prestat" en el que la portada en comptes de afegir-se a la xifra del subtrahend es resta de la xifra del minuend, es tatxa la xifra que hi ha i se'n escriu al damon una una unitat inferior, Te l'inconvenient que cal explicar casos particulars quant la xifra del minuend és zero. A la figura de la dreta s'il·lustra un exemple d'aquest algorisme.
La multiplicació (o producte)
[modifica]Multiplicar és una forma abreujada de realitzar una suma repetitiva de sumands iguals.
- a + a + a + a + a + a = 6 · a
Propietats del producte:
- Propietat commutativa: el producte no varia en canviar l'ordre dels factors.
- a · b = b · a
- Propietat associativa: el resultat del producte és independent de la forma en què s'agrupen els factors.
- (a · b) · c = a · (b · c)
La divisió
[modifica]Dividir és repartir a parts iguals o també partir en parts una quantitat.
La relació de divisibilitat
[modifica]Múltiples i divisors
[modifica]Nombres primers i compostos
[modifica]Els nombres naturals que no es poden dividir entre cap altre (tret de l'1) es diuen nombres primers. Els que sí que es poden dividir entre altres nombres diferents de l'1 es diuen nombres compostos.
Hi ha infinits nombres primers. Fixeu-vos que si n'hi hagués un nombre finit, es podrien multiplicar tots i al resultat sumar-li 1, però llavors s'obtindria un nombre que no seria divisible entre cap nombre primer; per tant, hi hauria d'haver un nombre primer diferent de tots que el dividís, perquè -altrament- ell mateix seria primer.
Descomposició d'un nombre en factors primers
[modifica]Tots els nombres naturals diferents de zero que no son nombres primers es poden expressar com a producte de nombres primers. El procés de trobar aquesta expressió es diu descomposició en factors primers.
El teorema fonamental de l'aritmètica diu que aquesta descomposició existeix i és única.
Aquest és un problema molt important en criptografia i hi ha molts algorismes per resoldre'l però si no és amb un ordinador quàntic no hi ha cap algorisme eficient publicat. Si els nombres són petits o tenen divisors petits un mètode factible és l'anomenada factorització per prova de divisions. Consisteix en provar si el nombre és divisible o no entre cada un dels nombres més petits que la seva arrel quadrada. De vegades es pot accelerar l'algorisme si els nombres són molt petits es pot tenir una llista dels nombres primers més petits que l'arrel quadrada del nombre a descompondre i llavors nomes cal provar si és divisible o no entre els nombres piers que es poden haver trobat primer, per exemple amb el sedàs d'Eratòstenes. A demés pels nombres primers més petits, si el nombre està escrit en base 10 (o en un altre base amb els canvis adequats), es pot aprofitat la informació que aporta l'escriptura del nombre en base 10 per estalviar la feina de calcular la divisió a base d'aplicar els criteris de divisibilitat. Per exemple si l'última xifra d'un nombre és parell, el nombr és múltiple de 2, si l'última xifra és 0 o 5 el nombre és múltiple de 5, si la suma de les xifres és múltiple de 3 el nombre és múltiple de 3. Vegeu l'article criteris de divisibilitat on hi ha criteris de divisibilitat per 16 nombres primers, es demostra cada un i s'explica com trobar-ne per a qualsevol nombre.
Mínim comú múltiple (m.c.m)
[modifica]El màxim comú divisor de dos o més nombres naturals és, el major divisor possible que ho és al mateix temps de tots ells. Si el màxim comú divisor de dos nombres és 1, aleshores aquests nombres es diuen coprimers o primers entre ells.
Tot i que es pot anar provant nombres naturals un per un fins trobar el m.c.d., existeixen mètodes generals per trobar-lo.
- Descomponent tots els nombres en factors primers es prenen els factors comuns amb el seu menor exponent. Multiplicant aquests factors comuns es troba el màxim comú divisor.
Per exemple, de les factoritzacions de 6936 i 1200,
6.936 = 23 · 3 · 172 1.200 = 24 · 3 · 52
es pot inferir que el seu m.c.d. és 23 · 3 = 24
- Si algun dels nombres és molt gran, aquest mètode no és operatiu perquè pot ser difícil conèixer-ne els possibles factors. En aquest cas es pot fer servir l'algorisme d'Euclides.
L'algorisme d'Euclides es basa en l'observació de què si un nombre a és divisor comú de altres dos b i c també és divisor comú del més petit dels dos i del residu de dividir el més gran entre el més petit. Fixeu-vos que si a és divisor comú de b i de c vol dir que existeixen dos nombres naturals b' i c' tals que b=b' ·a i c=c' ·c. expressant que:
on q és el quocient de dividir b entre c i r és el residu. D'aquí se'n dedueix que:
dividint els dos cantons entre a:
i restant als dos cantons c' ·q queda:
per tant a també és divisor de r (el resultat de dividir r entre a és un nombre natural). això permet transformar el problema de trobar el màxim comú divisor de b i c en el problema de trobar el màxim comú divisor de c i r. Llavors es pot dividir c entre r si el residu és 0 el màxim comú divisor és r si el residu no és zero es pot tornar a repetir el mateix emprant c en comptes de b i r en comtes de c i així successivament.
Per exemple, per trobar el màxim comú divisor de b = 945 i c = 651:
945 = 1×651 + 294
651 = 2×294 + 63
294 = 4×63 + 42
63 = 1×42 + 21
42 = 2×21 + 0 llavors mcd(945; 651) = 21 (l'últim residu no nul).
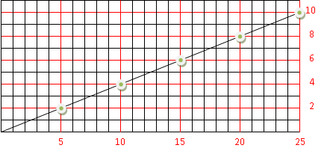
- Geomètricament, el màxim comú divisor de a i b és el nombre de punts de coordenades enteres que hi ha en el segment que unix els punts (0, 0) i (a, b), excloent el (0, 0). Vegeu figura de la dreta.
Cada nombre té molts divisors. El que menys en té, en té dos. Si agafem dos nombres és probable que tinguin divisors en comú. De vegades en tindran pocs, però de vegades en tindran molts. Per la utilitat que tindrà més endavant ens interessa poder localitzar quin és el més gran dels divisors que dos o més nombres tenen en comú.
Aquest nombre es coneix com a màxim comú divisor i se simbolitza amb les lletres mcd.
Pot passar que dos nombres només tinguin com a únic divisor comú el nombre 1. Quan passa això és diu que els dos nombres són primers entre ells.
Per localitzar el mcd de dos nombres podem fer-ho de tres formes diferents.
a) Utilitzant el significat de mcd.
Volem trobar el mcd de 10 i 24.
Escrivim tots els divisors de 10: 1, 2, 5 i 10. Escrivim tots els divisors de 24: 1, 2, 3, 4, 6, 8, 12 i 24.
Divisors comuns: 1 i 2. Divisor comú més gran: 2. Així doncs, 2 és el mcd entre 10 i 24 i ho escrivim així: mcd (24, 10) = 2.
Aquest mètode té l’inconvenient que no sempre és fàcil escriure tots els divisors d’un nombre. Per exemple, 720 té 24 divisors.
b) Utilitzant la descomposició en factors primers dels dos nombres.
Es comença descomponent en factors primers els nombres dels quals volem calcular el seu mcd.
24 2 10 2 12 2 5 5 6 2 1 3 3 1 Després observem quants factors primers hi ha i quantes vegades formen part de les dues descomposicions. En aquest cas, només tenen en comú el factor 2 i una sola vegada.
El producte de tots els factors primers repetits és el màxim comú divisor.
En aquest cas, mcd (24, 10) = 2
Aquest mètode és força pràctic, però té l’inconvenient que no sempre sabem trobar la descomposició en factors primers dels dos nombres.
c) Mètode de les divisions o mètode d’Euclides.
Trobar el mcd de dos nombres va ser un problema que ja van resoldre els matemàtics grecs. Euclides d’Alexandria (c. 365-275 aC) va idear un mètode que utilitza divisions per trobar el mcd.
Si hem de trobar el mcd de 24 i 10 dividim 24 per 10:
24 10 4 2 Després dividim 10 pel residu d’aquesta divisió:
10 4 2 2 Després dividim 4 pel residu d’aquesta divisió:
4 2 0 2 Com que aquesta divisió ha donat com a residu 0, el 2, l’últim divisor utilitzat, és el mcd.
mcd (24, 10) = 2
Per aplicar aquest mètode ens cal, només, saber fer divisions.
Exemple:
Calcularem el mcd de 108 i 96
a) Utilitzant el significat de mcd:
Divisors de 96: 1, 2, 4, 6, 8, 12, 16, 24, 32, 48, 96. Divisors de 108: 1, 2, 4, 6, 12, 18, 36, 54, 108.
Divisors comuns: 2, 4, 6, 12
mcd (108, 96) = 12
b) Utilitzant la descomposició en factors:
108 2 96 2 54 2 48 2 27 3 24 2 9 3 12 2 3 3 6 2 1 1 3 3 1 Observem que els factors repetits són 2, que apareix dues vegades repetit, i un factor 3.
Per tant mcd (108, 96) = 2 · 2 · 3 = 22 · 3 = 12
c) Mètode de les divisions:
108 96 96 12 12 1 0 8 Per tant, com que la segona divisió ha donat exacte, mcd (108, 96) = 12
Ordre de les operacions
[modifica]- Parèntesis.
- Multiplicació i divisió.
- Suma i resta.
Notes
[modifica]- ↑ Calligraphia et tipographia, arithmetica et numerica, chronologia Josep Balcells i Reig, Universidad de Barcelona, pàgina 229
- ↑ Temari Oposicions. Vol.ii. Cos de Mestres. EducaciÓ PrimÀria Academia Ariete, S.L, pàgina 316




