Cinemàtica/Conceptes bàsics
Sistema de referència
[modifica]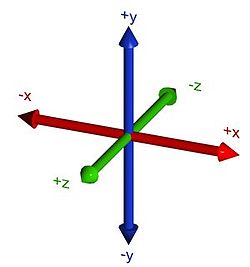
En cinemàtica, un sistema de referència es un conjunt de convencions per poder mesurar la posició d'un objecte en el temps i l'espai, que en la mecànica clàssica són magnituds infinites. A la vida quotidiana fem servir també sovint referències per situar-nos, com per exemple quan expliquem a algú que ha de tirar cap a la dreta, des del punt en què es troba i mirant a la plaça.
L'objecte d'estudi és sempre al mateix punt absolut es miri desde la referència que es miri, però necessitem posar-nos d'acord en una referència per a poder-nos comunicar. Per exemple, Barcelona és al nord si prenc coma referència Tarragona però al sud si la meva referència és Girona. Així doncs, no em serveix de res dir "cent quilómetres recte cap al nord" si no especifico quina és la meva referència, és a dir, un punt d'origen a partir del qual faig els cent quilómetres, i uns vectors, en aquest cas el "nord" seria un de vertical que té sentit positiu quan va cap amunt, dient tot això ara sí podem quedar tots al mateix lloc. Evidentement, per definir el mateix punt es podria usar una altra referència (un altre lloc de partida, per exemple) però aleshores per situar-lo en principi no ens valdria la mateixa descreipció, "cent quilómetres recte cap al nord", sinó una altra, com per exemple, "un quilómetre al sud i cinquanta a l'est".
El primer element és l'origen de la referència. Consisteix en un punt escollit arbitràriament, pertanyent o no a un objecte físic, mòbil o estàtic, a partir del qual es prenen totes les mesures.
El segon element són els eixos de coordenades. Els eixos de coordenades són vectors (rectes que tenen un sentit determinat) no paral·les que tenen tots com a origen el punt de referència.
Quan estudiem un espai d'una dimensió, és a dir, un cos que es mou sempre dins d'una recta, podem prendre com a referència un origen que sigui un punt de la recta i un sol eix de coordenades, que surti d'aquest punt i estigui sobre la recta del moviment. També podem fer servir com a origen un altre punt exterior a la recta, i dos o tres eixos que no coincideixin amb la recta, i obtindrem exactament els mateixos resultats però amb càlculs més complexos.
Quan el cos o punt es mou en un pla, és a dir, en dues dimensions, el sistema de referència més senzill que podem utilitzar és un format per dos vectors que peratnyin al pla i que es tallin en un punt d'aquest pla, punt que considerarem origen de la referència. Si els vectors són perpendiculars obtindrem equacions més simples i més intuitives que si no ho són.
En un espai tridimensional necessitem almenys tres vectors que es tallin en un punt origen. També és aconsellable en general prendre vectors que siguin perpendiculats entre ells i tals que tots tres surtin de l'origen cap enfora, és a dir, que multiplicant dos dels eixos obtinguem sempre el tercer eix i no el tercer amb sentit invers. Normalment es considera que un eix indicarà la distància dreta-esquerra del cos respecte del punt que prenem com a origen, un altre eix indica la profunditat i un tercer l'alçada.
Els eixos de coordenades més usuals a les matemàtiques més sencilles se solen anomenar (x,y,z) però als que podem posar els noms que volguem. Típicament es considera l'eix x horitzontal, positiu cap a la dreta i negatiu cap a l'esquerra; l'eix y vertical, positiu cap amunt i negatiu cap avall; i l'eix z mesura la profunditat, positiu quan s'apropa i negatiu quan s'enfonsa.
Quan s'estudien moviments respecte a la superfície de la Terra, s'acostuma a fer passar l'eix y o l'eix z pel centre de la Terra, amb l'origen de coordenades situat a la superfície, i a considerar la terra "plana" (per a la majoria de moviments, excepte per exemple el d'un avió intercontinental, el radi de curvatura de la terra és tan gran respecte al moviment que podem considerar que és infinit, i per tant la superfície de la terra no esfèrica i en conseqüència que no hi ha moviment vertical si no "saltem" o ens "enfonsem" en la terra).
També podem prendre un instant de temps com a referènciaa, a partir del qual es mesura el temps que passa el moviment. Aquest instant acostuma a coincidir amb un succés concret, com el naixement de Crist que s'empra com a origen al calendari cristià. En cinemàtica l'origen temporal coincideix moltes vegades amb l'inici del moviment que s'estudia.
Aquests tres elements: punt de referència, eixos de coordenades i origen temporal, formen el sistema de referència. Però per poder emprar un sistema de referència calen unes unitats de mesura que ens serveixin per quantificar. Les unitats són convencionals, i es defineixen agafant com a referència elements físicament constants. A un conjunt d'unitats i les seves relacions se l'anomena sistema d'unitats. En el Sistema Internacional d'Unitats o S.I., s'empra el metre com unitat de l'espai i el segon com unitat del temps.
El sistema de referència depèn del model físic que s'estudia i s'escull de manera que faci l'estudi més fàcil. Els resultats finals són independents del sistema escollit. A vegades convé emprar diferents sistemes de referència pel mateix problema. Ena quest casos es creen sistemes d'equacions que tradueixen posicions explicades en una referència per a passar-les a una altra.
Moviment
[modifica]El moviment és un procés pel qual, almenys un dels elements del sistema que es considera, canvia de posició en l'espai o repecte de si mateix. Quan el cos o el punt que estudiem canvia de posició respecte a l'espai diem que ha fet un moviment lineal, que pot ser rectilini, circular, parabòlic, caòtic, etc. mentre que quan el cos es mou sense canviar de posició diem que es tracta d'un moviment angular. Un mateix cos pot fer diversos moviments alhora, per exemple, un vaixell es pot balancejar (moviment angular) a banda i banda, pot pujar i baixar el morro a mesura que topa amb les ones (un altre d'angular, en un altre eix) i al mateix temps pot estar desplaçant-se per anar d'un punt a un altre.
Tot cos en moviment lineal descriu una trajectòria. En el cas del vaixell la trajectòria seria el que queda marcat a la mar quan es trasllada.
Trajectòria
[modifica]
La trajectòria és el conjunt de totes les posicions per les quals passa un cos en moviment.
Matemàticament si tenim definida la posició en funció del temps:
s'aïlla a qualsevol de les tres expressions:
Les altres dues expressions es defineixen en funció d'aquesta:
Com que tenim dues equacions en un espai tridimensional, aquest conjunt té un grau de llibertat, i per tant defineix una línia, que serà la trajectòria del cos en l'espai.
Segons la mecànica clàssica la trajectòria d'un cos puntual sempre serà una línia contínua. La física moderna, però, ha trobat situacions on això no ocorre. Per exemple, la trajectòria d'un electró dins d'un àtom és probabilística, i correspon a un volum.







