Matemàtiques (nivell ESO)/Aplicacions dels polinomis

Els polinomis tenen moltes aplicacions, no només als diversos àmbits de la ciència, sinó també al dia a dia.

Interès compost[modifica]

Per calcular el capital final produït per un cert capital a interès compost durant una sèrie d'anys, es fa servir la fórmula següent

CF=CI\cdot (1+i)^{n}

Correspon a un monomi de dues variables.

Coloració de grafs[modifica]

Coloració de grafs. El polinomi cromàtic indica el nombre de maneres de colorar un graf a partir d'un nombre fixat de colors.

Alguns grafs molt coneguts i el seu polinomi cromàtic

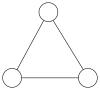
	El triangle $K_{3}$	$t(t-1)(t-2)\$
	Graf complet $K_{n}$	$t(t-1)(t-1)\dots (t-(n-1))\$
	Cicle $C_{n}$	$(t-1)^{n}+(-1)^{n}(t-1)\$
	Graf de Petersen	$t(t-1)(t-2)(t^{7}-12t^{6}+67t^{5}-230t^{4}+529t^{3}-814t^{2}+775t-352)$
	Graf llibre $B_{n}$	$(t-1)t(t^{2}-3t+3)^{n}\$
	Graf centpeus	$(t-1)^{2n-1}t\$
	Graf camí $P_{n}$	$t(t-1)^{n-1}\$
	Graf estrella $S_{n}$	$t(t-1)^{n-1}\$
	Graf roda $W_{n}$	$t\left[(t-2)^{n-1}-(-1)^{n}(t-2)\right]$

Calculant el valor numèric de qualsevol d'aquests polinomis per a un cert valor de la indeterminada, el resultat és el nombre de coloracions possibles per al graf associat usant tants de colors com indiqui el valor d'aquesta indeterminada. Per exemple, agafant el graf estrella de 3 vèrtexs i 4 colors, $S_{3}(4)=4(4-1)^{3-1}=36$ , de manera que aquest graf admet 36 coloracions diferents.

Interpolació polinòmica[modifica]

Aproximació de funcions[modifica]

Oftalmologia i optometria[modifica]

Descripció d'aberracions de la còrnia o de lens en oftalmologia i optometria respecte d'una forma esfèrica ideal, que condueixen a errors de refracció. Per a aquest propòsit s'usen els anomenats polinomis de Zernicke.

Els primers polinomis radials no nuls emprats en la definició dels polinomis de Zernike són:^[1]

$R_{0}^{0}(\rho )=1$

$R_{1}^{1}(\rho )=\rho$

$R_{2}^{0}(\rho )=2\rho ^{2}-1$

$R_{2}^{2}(\rho )=\rho ^{2}$

$R_{3}^{1}(\rho )=3\rho ^{3}-2\rho$

$R_{3}^{3}(\rho )=\rho ^{3}$

$R_{4}^{0}(\rho )=6\rho ^{4}-6\rho ^{2}+1$

$R_{4}^{2}(\rho )=4\rho ^{4}-3\rho ^{2}$

$R_{4}^{4}(\rho )=\rho ^{4}$

Els 9 primers polinomis de Zernike són:

Polinomi de Zernike	Aberracions
$z_{0}=1\$	piston
$z_{1}=x\$	x-tilt
$z_{2}=y\$	y-tilt
$z_{3}=-1+2(x^{2}+y^{2})\$	focus
$z_{4}=x^{2}-y^{2}\$	astigmatisme a 0° i focus
$z_{5}=2xy\$	astigmatisme a 45° i focus
$z_{6}=-2x+3x(x^{2}+y^{2})\$	coma i x-tilt
$z_{7}=-2y+3y(x^{2}+y^{2})\$	coma i y-tilt
$z_{8}=1-6(x^{2}+y^{2})+6(x^{2}+y^{2})^{2}\$	esfèric i focus